
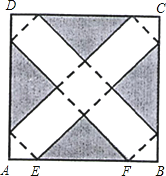
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A.B.C.D四个顶点正好重合于上底面上一点).已知E、F在AB边上,是被剪去的一个等腰直角三角形斜边的两个端点,设AE=BF=x(cm).
(1)若折成的包装盒恰好是个正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12,求四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
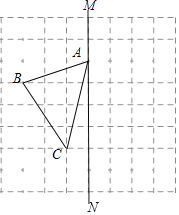
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上)
(1)△ABC的面积为 ;
(2)在图中作出△ABC关于直线MN的对称图形△A'B'C';
(3)在MN上找一点P,使得PB+PC的距离最短,这个最短距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
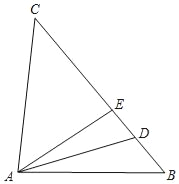
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
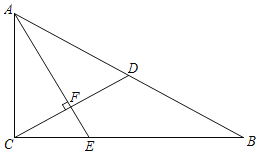
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD于点F,交CB于点E,且∠EAB=∠DCB.
(1)求∠B的度数:
(2)求证:BC=3CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的两个端点坐标分别为(﹣2,1)和(2,3).
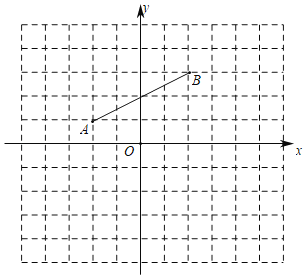
(1)在图中分别画出线段AB关于x轴的对称线段A1B1,并写出A1、B1的坐标.
(2)在x轴上找一点C,使AC+BC的值最小,在图中作出点C,并直接写出点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com