
ЁОЬтФПЁПКажагаШєИЩУЖКкЦхКЭАзЦхЃЌетаЉЦхГ§беЩЋЭтЮоЦфЫћВюБ№ЃЌЯжШУбЇЩњНјааУўЦхЪдбщЃКУПДЮУўГівЛУЖЦхЃЌМЧТМбеЩЋКѓЗХЛивЁдШЃЎжиИДНјааетбљЕФЪдбщЕУЕНвдЯТЪ§ОнЃК
УўЦхЕФДЮЪ§n | 100 | 200 | 300 | 500 | 800 | 1000 |
УўЕНКкЦхЕФДЮЪ§m | 24 | 51 | 76 | 124 | 201 | 250 |
УўЕНКкЦхЕФЦЕТЪ | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
ЃЈ1ЃЉИљОнБэжаЪ§ОнЙРМЦДгКажаУўГівЛУЖЦхЪЧКкЦхЕФИХТЪЪЧЁЁ ЁЁЃЛЃЈОЋШЗЕН0.01ЃЉ
ЃЈ2ЃЉШєКажаКкЦхгыАзЦхЙВга4УЖЃЌФГЭЌбЇвЛДЮУўГіСНУЖЦхЃЌЧыМЦЫуетСНУЖЦхбеЩЋВЛЭЌЕФИХТЪЃЌВЂЫЕУїРэгЩ
ЁОД№АИЁПЃЈ1ЃЉ0.25ЃЛЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
![]() ДѓСПжиИДЪдбщЯТУўЧђЕФЦЕТЪПЩвдЙРМЦУўЧђЕФИХТЪ;
ДѓСПжиИДЪдбщЯТУўЧђЕФЦЕТЪПЩвдЙРМЦУўЧђЕФИХТЪ;
![]() ЛЪїзДЭМСаГіЫљгаЕШПЩФмНсЙћЃЌдйевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌИљОнИХТЪЙЋЪНЧѓНт.
ЛЪїзДЭМСаГіЫљгаЕШПЩФмНсЙћЃЌдйевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌИљОнИХТЪЙЋЪНЧѓНт.
ЃЈ1ЃЉИљОнБэжаЪ§ОнЙРМЦДгКажаУўГівЛУЖЦхЪЧКкЦхЕФИХТЪЪЧ0.25ЃЌ
ЙЪД№АИЮЊЃК0.25ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊЃЌКкЦхЕФИіЪ§ЮЊ4ЁС0.25=1ЃЌдђАзЦхзгЕФИіЪ§ЮЊ3ЃЌ
ЛЪїзДЭМШчЯТЃК
гЩБэПЩжЊЃЌЫљгаЕШПЩФмНсЙћЙВга12жжЧщПіЃЌ
ЦфжаетСНУЖЦхбеЩЋВЛЭЌЕФга6жжНсЙћЃЌ
ЫљвдетСНУЖЦхбеЩЋВЛЭЌЕФИХТЪЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
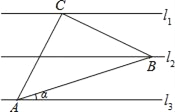
ЁОЬтФПЁПШчЭМЃЌвбжЊl1ЁЮl2ЁЮl3ЃЌЯрСкСНЬѕЦНаажБЯпМфЕФОрРыЯрЕШЃЌШєЕШбќжБНЧШ§НЧаЮABCЕФжБНЧЖЅЕуCдкl1ЩЯЃЌСэСНИіЖЅЕуAЃЌBЗжБ№дкl3ЃЌl2ЩЯЃЌдђsinІСЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЧЪаЮЊДДНЈЙњМвЮРЩњГЧЪаЃЌашвЊЙКТђМзЁЂввСНжжРраЭЕФЗжРрРЌЛјЭАЃЈШчЭМЫљЪОЃЉЃЌОнЕїВщИУГЧЪаЕФAЁЂBЁЂCШ§ИіЩчЧјЛ§МЋЯьгІКХВЂЙКТђЃЌОпЬхЙКТђЕФЪ§КЭзмМлШчБэЫљЪОЃЎ
ЩчЧј | МзаЭРЌЛјЭА | вваЭРЌЛјЭА | змМл |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
ЃЈ1ЃЉдЫгУБОбЇЦкЫљбЇжЊЪЖЃЌСаЖўдЊвЛДЮЗНГЬзщЧѓМзаЭРЌЛјЭАЁЂвваЭРЌЛјЭАЕФЕЅМлУПЬзЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉАДвЊЧѓИїИіЩчЧјСНжжРраЭЕФРЌЛјЭАЖМвЊгаЃЌдђaЃНЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBЃЌCЖМдкХзЮяЯпy=ax2Љ2amx+am2+2mЉ5ЃЈЦфжаЉ![]() ЃМaЃМ0ЃЉЩЯЃЌABЁЮxжсЃЌЁЯABC=135ЁуЃЌЧвAB=4ЃЎ
ЃМaЃМ0ЃЉЩЯЃЌABЁЮxжсЃЌЁЯABC=135ЁуЃЌЧвAB=4ЃЎ
ЃЈ1ЃЉЬюПеЃКХзЮяЯпЕФЖЅЕузјБъЮЊ ЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЧѓЁїABCЕФУцЛ§ЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ3ЃЉШєЁїABCЕФУцЛ§ЮЊ2ЃЌЕБ2mЉ5ЁмxЁм2mЉ2ЪБЃЌyЕФзюДѓжЕЮЊ2ЃЌЧѓmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
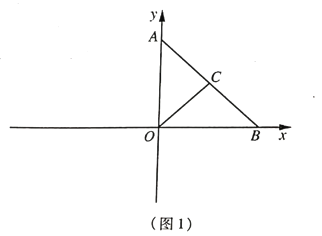
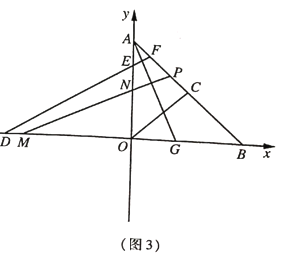
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЮЊзјБъдЕуЃЌ
ЮЊзјБъдЕуЃЌ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() дк
дк![]() жсЩЯ(Еу
жсЩЯ(Еу![]() дкЕу
дкЕу![]() ЕФгвВр)ЃЌЕу
ЕФгвВр)ЃЌЕу![]() дк
дк![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
(1)ШчЭМ1ЃЌЧѓЕу![]() ЕФзнзјБъЃЛ
ЕФзнзјБъЃЛ
(2)ШчЭМ2ЃЌЕу![]() дк
дк![]() жсЩЯ(Еу
жсЩЯ(Еу![]() дкЕу
дкЕу![]() ЕФзѓВр)ЃЌЕу
ЕФзѓВр)ЃЌЕу![]() дк
дк![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЛШє
ЃЛШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]()
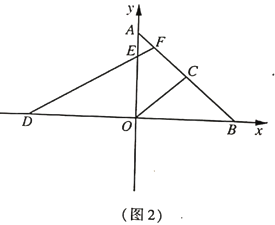
(3)ШчЭМ3ЃЌдк(2)ЕФЬѕМўЯТЃЌ![]() ЪЧ
ЪЧ![]() ЕФНЧЦНЗжЯпЃЌЕу
ЕФНЧЦНЗжЯпЃЌЕу![]() гыЕу
гыЕу![]() Йигк
Йигк![]() жсЖдГЦЃЌЙ§Еу
жсЖдГЦЃЌЙ§Еу![]() зї
зї![]() ЗжБ№НЛ
ЗжБ№НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+![]() ЃЈaЃО0ЃЌbЃМ0ЃЉЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуA
ЃЈaЃО0ЃЌbЃМ0ЃЉЕФЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуA
ЃЈ1ЃЉЕБa=![]() ЪБЃЌЧѓЕуAЕФзјБъЃЛ
ЪБЃЌЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЙ§ЕуAЕФжБЯпy=x+kгыЖўДЮКЏЪ§ЕФЭМЯѓЯрНЛгкСэвЛЕуBЃЌЕБbЁнЉ1ЪБЃЌЧѓЕуBЕФКсзјБъmЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
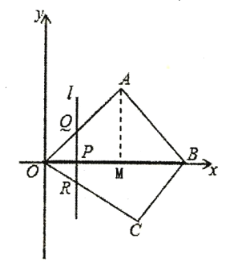
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЪЧзјБъдЕуЃЌЕу
ЪЧзјБъдЕуЃЌЕу![]() дкЕквЛЯѓЯоЃЌЕу
дкЕквЛЯѓЯоЃЌЕу![]() дкЕкЫФЯѓЯоЃЌЕу
дкЕкЫФЯѓЯоЃЌЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЎ
жсЕФе§АыжсЩЯЃЎ![]() Чв
Чв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФГЄЗжБ№ЪЧЖўдЊвЛДЮЗНГЬзщ
ЕФГЄЗжБ№ЪЧЖўдЊвЛДЮЗНГЬзщ![]() ЕФНтЃЈ
ЕФНтЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓЕу![]() КЭЕу
КЭЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЈЕу
ЩЯЕФвЛИіЖЏЕуЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гы
гы![]() жсЦНааЃЌжБЯп
жсЦНааЃЌжБЯп![]() НЛБп
НЛБп![]() ЛђБп
ЛђБп![]() гкЕу
гкЕу![]() ЃЌНЛБп
ЃЌНЛБп![]() ЛђБп
ЛђБп![]() гкЕу
гкЕу![]() ЃЎЩшЕу
ЃЎЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФГЄЖШЮЊ
ЕФГЄЖШЮЊ![]() ЃЎвбжЊ
ЃЎвбжЊ![]() ЪБЃЌжБЯп
ЪБЃЌжБЯп![]() ЧЁКУЙ§Еу
ЧЁКУЙ§Еу![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ14ЗжЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=mx2Љ8mx+4m+2ЃЈmЃО2ЃЉгыyжсЕФНЛЕуЮЊAЃЌгыxжсЕФНЛЕуЗжБ№ЮЊBЃЈx1ЃЌ0ЃЉЃЌCЃЈx2ЃЌ0ЃЉЃЌЧвx2Љx1=4ЃЌжБЯпADЁЮxжсЃЌдкxжсЩЯгавЛЖЏЕуEЃЈtЃЌ0ЃЉЙ§ЕуEзїЦНаагкyжсЕФжБЯпlгыХзЮяЯпЁЂжБЯпADЕФНЛЕуЗжБ№ЮЊPЁЂQЃЎ
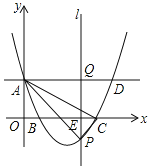
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБ0ЃМtЁм8ЪБЃЌЧѓЁїAPCУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕБtЃО2ЪБЃЌЪЧЗёДцдкЕуPЃЌЪЙвдAЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃПШєДцдкЃЌЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
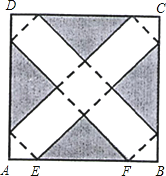
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ24cmЕФе§ЗНаЮжНЦЌABCDЩЯЃЌМєШЅЭМжавѕгАВПЗжЕФЫФИіШЋЕШЕФЕШбќжБНЧШ§НЧаЮЃЌдйбиЭМжаЕФащЯпелЦ№ЃЌелГЩвЛИіГЄЗНЬхаЮзДЕФАќзАКаЃЈAЃЎBЃЎCЃЎDЫФИіЖЅЕуе§КУжиКЯгкЩЯЕзУцЩЯвЛЕуЃЉЃЎвбжЊEЁЂFдкABБпЩЯЃЌЪЧБЛМєШЅЕФвЛИіЕШбќжБНЧШ§НЧаЮаББпЕФСНИіЖЫЕуЃЌЩшAE=BF=xЃЈcmЃЉЃЎ
ЃЈ1ЃЉШєелГЩЕФАќзАКаЧЁКУЪЧИіе§ЗНЬхЃЌЪдЧѓетИіАќзАКаЕФЬхЛ§VЃЛ
ЃЈ2ЃЉФГЙуИцЩЬвЊЧѓАќзАКаЕФБэУцЃЈВЛКЌЯТЕзУцЃЉУцЛ§SзюДѓЃЌЪдЮЪxгІШЁКЮжЕЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com