
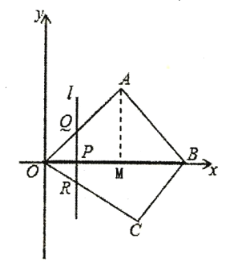
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 在第一象限,点
在第一象限,点![]() 在第四象限,点
在第四象限,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.![]() 且
且![]() ,
,![]() ,
,![]() 的长分别是二元一次方程组
的长分别是二元一次方程组![]() 的解(
的解(![]() ).
).
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 的直线
的直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,交边
,交边![]() 或边
或边![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() .已知
.已知![]() 时,直线
时,直线![]() 恰好过点
恰好过点![]() .
.
①当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②当![]() 时,求点
时,求点![]() 的横坐标
的横坐标![]() 的值.
的值.
【答案】(1)A(3,3),B(6,0);(2)当![]() 时,
时,![]() ;(3)满足条件的P的坐标为(2,0)或
;(3)满足条件的P的坐标为(2,0)或![]()
【解析】
(1)解方程组得到OB,OC的长度,得到B点坐标,再根据△OAB是等腰直角三角形,解出点A的坐标;
(2)①根据坐标系中两点之间的距离,QR的长度为点Q与点R纵坐标之差,根据OC的函数解析式,表达出点R坐标,根据△OPQ是等腰直角三角形得出点Q坐标,表达m即可;
②根据直线l的运动时间分类讨论,分别求出直线AB,直线BC的解析式,再由QR的长度为点Q与点R纵坐标之差表达出m的函数解析式,当![]() 时,列出方程求解.
时,列出方程求解.
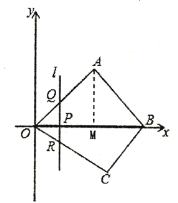
解:(1)如图所示,过点A作AM⊥OB,交OB于点M,
解二元一次方程组![]() ,得:
,得:![]() ,
,
∵![]() ,
,
∴OB=6,OC=5
∴点B的坐标为(6,0)
∵∠OAB=90°,OA=AB,
∴△OAB是等腰直角三角形,∠AOM=45°,
根据等腰三角形三线合一的性质可得![]() ,
,
∵∠AOM=45°,则∠OAM=90°-45°=45°=∠AOM,
∴AM=OM=3,所以点A的坐标为(3,3)
∴A(3,3),B(6,0)
(2)①由(1)可知,∠AOM=45°,
又PQ⊥OP,
∴△OPQ是等腰直角三角形,
∴PQ=OP=t,
∴点Q(t,t)
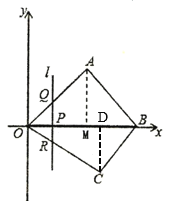
如下图,过点C作CD⊥OB于点D,
∵![]() 时,直线
时,直线![]() 恰好过点
恰好过点![]() ,
,
∴OD=4,OC=5
在Rt△OCD中,CD=![]()
∴点C(4,-3)
设直线OC解析式为y=kx,
将点C代入得-3=4k,
∴![]() ,
,
∴![]() ,
,
∴点R(t,![]() )
)
∴![]()
故当![]() 时,
时,![]()
②设AB解析式为![]()
将A(3,3)与点B(6,0)代入得
![]() ,解得
,解得![]()
所以直线AB的解析式为![]() ,
,
同理可得直线BC的解析式为![]()
当![]() 时,若
时,若![]() ,则
,则![]() ,解得t=2,∴P(2,0)
,解得t=2,∴P(2,0)
当![]() 时,
时,![]() ,若
,若![]() ,即
,即![]() ,解得t=10(不符合,舍去)
,解得t=10(不符合,舍去)
当![]() 时,Q(t,-t+6),R(t,
时,Q(t,-t+6),R(t,![]() )
)
∴![]()
若![]() ,即
,即![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
综上所述,满足条件的P的坐标为(2,0)或![]() .
.


科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
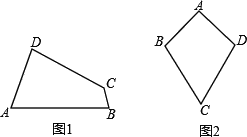
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=78°,∠B=82°,则∠C=_________,∠D=__________
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例(提示:举反例可画图并说明)
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=![]() ,AD=
,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
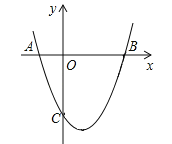
【题目】如图,抛物线与x轴的交点分别为A、B,与y轴的负半轴交于点C.已知抛物线的顶点坐标为(1,﹣4),点B的坐标(3,0).
(1)求该抛物线的解析式.
(2)在该函数图象上能否找到一点P,使PO=PC?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,同时在甲服装店租用2件和乙服装店租用3件共需280元,在甲服装店租用4件和乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,则超出5件的部分可按原价的六折进行优惠;设需要租用![]() (
(![]() )件服装,选择甲店则需要
)件服装,选择甲店则需要![]() 元,选择乙店则需要
元,选择乙店则需要![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
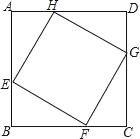
【题目】如图,在正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边上的动点,且AE=BF=CG=DH.
(1)求证:△AEH≌△CGF;
(2)在点E、F、G、H运动过程中,判断直线EG是否经过某一个定点,如果是,请证明你的结论;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠CAB=30°,DE⊥AC于E,且AE=CE,若DE=5,EB=12,求四边形ABCD的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com