
【题目】如图,四边形![]() 为半径为
为半径为![]() 的
的![]() 的内接四边形,若
的内接四边形,若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的直径为( )
的直径为( )
A.4B.![]() C.8D.
C.8D.![]()
【答案】C
【解析】
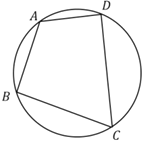
取![]() 的圆心O,连接OA、OB、OC、OD,过点O作OE⊥CD,OF⊥BC,OG⊥AD,垂足分别为E,F,G,先证得∠AOB=60°及∠COD =120°,可得AOD+∠BOC=180°,再利用垂径定理可得∠AOG+∠BOF=90°,最后通过证△BOF≌△OAG得OF=AG=2,再利用勾股定理求解即可.
的圆心O,连接OA、OB、OC、OD,过点O作OE⊥CD,OF⊥BC,OG⊥AD,垂足分别为E,F,G,先证得∠AOB=60°及∠COD =120°,可得AOD+∠BOC=180°,再利用垂径定理可得∠AOG+∠BOF=90°,最后通过证△BOF≌△OAG得OF=AG=2,再利用勾股定理求解即可.
解:如图,取![]() 的圆心O,连接OA、OB、OC、OD,过点O作OE⊥CD,OF⊥BC,OG⊥AD,垂足分别为E,F,G,
的圆心O,连接OA、OB、OC、OD,过点O作OE⊥CD,OF⊥BC,OG⊥AD,垂足分别为E,F,G,

∵OA=OB=AB=R,
∴△AOB为等边三角形,
∴∠AOB=60°,
∵OE⊥CD,![]() ,
,
∴![]() ,
,
在Rt△COE中,

∴∠COE=60°,
∴∠COD=2∠COE=120°,
∴∠AOD+∠BOC=360°﹣∠COD﹣∠AOB=180°,
∵OF⊥BC,OG⊥AD,
∴AG=![]() AD=2,BF=
AD=2,BF=![]() BC=2
BC=2![]() ,∠AOG=
,∠AOG=![]() ∠AOD,∠BOF=
∠AOD,∠BOF=![]() ∠BOC,
∠BOC,
∴∠AOG+∠BOF=![]() (∠AOD+∠BOC)=90°
(∠AOD+∠BOC)=90°
又∵∠AOG+∠OAG=90°,
∴∠BOF=∠OAG,
∵∠BOF=∠OAG,∠BFO=∠OGA=90°,OB=OA,
∴△BOF≌△OAG(AAS),
∴OF=AG=2,
在Rt△BOF中,![]() ,
,
∴![]() 的直径=2OB=8,
的直径=2OB=8,
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以![]() cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC
cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC![]() CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )
CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是 ( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌![]() ,小明在斜坡上
,小明在斜坡上![]() 处测得标识牌顶部
处测得标识牌顶部![]() 的仰角为
的仰角为![]() ,沿斜坡走下来在地面
,沿斜坡走下来在地面![]() 处测得标识牌底部
处测得标识牌底部![]() 的仰角为60°,已知斜坡
的仰角为60°,已知斜坡![]() 的坡角为30°,
的坡角为30°,![]() 米. 则标识牌
米. 则标识牌![]() 的高度是米__________.
的高度是米__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,抛物线的顶点记为
两点,抛物线的顶点记为![]() .其对称轴与
.其对称轴与![]() 轴的交点记为
轴的交点记为![]() ;
;
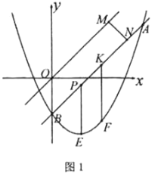
(1)如图1,在线段![]() 上有两个动点
上有两个动点![]() 、
、![]() ,且
,且![]() ,作
,作![]() 轴,分别交抛物线于点
轴,分别交抛物线于点![]() 、
、![]() ,过点
,过点![]() 作另一条直线
作另一条直线![]() ,当
,当![]() 取得最大值时,有一动点
取得最大值时,有一动点![]() 从
从![]() 出发沿某条路径以1个单位每秒的速度先运动到直线
出发沿某条路径以1个单位每秒的速度先运动到直线![]() 上的点
上的点![]() 处,再沿垂直于
处,再沿垂直于![]() 的方向以1个单位每秒的速度从点
的方向以1个单位每秒的速度从点![]() 运动到
运动到![]() 上
上![]() 点处,最后以
点处,最后以![]() 个单位每秒的速度从点
个单位每秒的速度从点![]() 回到点
回到点![]() ,运动停止,请求出满足条件的
,运动停止,请求出满足条件的![]() 点坐标及动点
点坐标及动点![]() 运动总时间的最小值;
运动总时间的最小值;
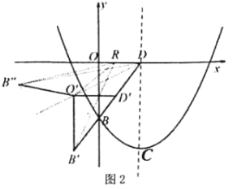
(2)如图2,连接![]() ,将
,将![]() 沿射线
沿射线![]() 平移得
平移得![]() ,当
,当![]() 恰好落在∠BDO的角平分线上时,在
恰好落在∠BDO的角平分线上时,在![]() 轴上取一点
轴上取一点![]() ,再将
,再将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 为等腰三角形时,求出
为等腰三角形时,求出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=![]() .
.

(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
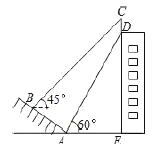
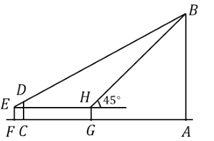
【题目】小明准备利用所学的知识测量旗杆![]() 的高度.他设计了如下的测量方案:选取一个合适观测点,在地面
的高度.他设计了如下的测量方案:选取一个合适观测点,在地面![]() 处垂直地面竖立高度为2米的标杆
处垂直地面竖立高度为2米的标杆![]() ,小明调整自己的位置到
,小明调整自己的位置到![]() 处,使得视线与
处,使得视线与![]() 、
、![]() 在同一直线上,此时测得
在同一直线上,此时测得![]() 米,然后小明沿着
米,然后小明沿着![]() 方向前进11米到
方向前进11米到![]() 处,利用随身携带的等腰直角三角形测得
处,利用随身携带的等腰直角三角形测得![]() 点的仰角为45°,已知小明眼睛到地面距离为1.5米(
点的仰角为45°,已知小明眼睛到地面距离为1.5米(![]() 米),请你根据题中所给的数据计算旗杆的高度.
米),请你根据题中所给的数据计算旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
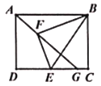
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
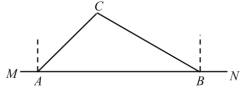
【题目】如图,某公路局施工队要修建一条东西方向的公路![]() ,已知
,已知![]() 点周围100米范围内为古建筑保护群,在
点周围100米范围内为古建筑保护群,在![]() 上的点
上的点![]() 处测得
处测得![]() 在
在![]() 的北偏东
的北偏东![]() 方向上,从
方向上,从![]() 向东走400米到达
向东走400米到达![]() 处,测得
处,测得![]() 在点
在点![]() 的北偏西
的北偏西![]() 方向上.(参考数据:
方向上.(参考数据:![]() ,
,![]() )
)
(1)![]() 是否穿过古建筑保护群?为什么?
是否穿过古建筑保护群?为什么?
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高![]() ,则原计划完成这项工程需要多少天?
,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,如果
运动,如果![]() 、
、![]() 两点同时出发,
两点同时出发,![]() 的速度为1个单位/秒.
的速度为1个单位/秒.![]() 在
在![]() 上的速度为1个单位/秒,在
上的速度为1个单位/秒,在![]() 上的速度为
上的速度为![]() 个单位/秒.设出发时间为
个单位/秒.设出发时间为![]() ,记
,记![]() 的面积
的面积![]() 的函数图象为
的函数图象为![]() .
.

(1)当![]() 时,
时,![]() 的长是_________;
的长是_________;
(2)若直线![]() 与
与![]() 有两个交点,则
有两个交点,则![]() 的取值范围为_________.
的取值范围为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com