
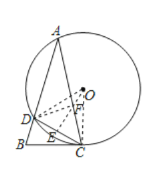
【题目】如图,△ABC的点A,C在⊙O上,⊙O与AB相交于点D,连接CD,∠A=30°,DC=![]() .
.

(1)求圆心O到弦DC的距离;
(2)若∠ACB+∠ADC=180°,求证:BC是⊙O的切线.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)连接OD,OC,过O作OE⊥OC于E,得到△OCD是等边三角形,求得OD=OC=CD=![]() ,解直角三角形即可得到结论;
,解直角三角形即可得到结论;
(2)由(1)得,△ODC是等边三角形,求得∠OCD=60°,根据相似三角形的性质得到∠A=∠BCD=30°,求得∠OCB=90°,于是得到BC是⊙O的切线.
解:(1)连接OD,OC,过O作OE⊥OC于E,
∵∠A=30°,
∴∠DOC=60°,
∵OD=OC,CD=![]() ,
,
∴△OCD是等边三角形,
∴OD=OC=CD=![]() ,
,
∵OE⊥DC,
∴DE=![]() ,∠DEO=90°,∠DOE=30°,
,∠DEO=90°,∠DOE=30°,
∴OE=![]() DE=
DE=![]() ,
,
∴圆心O到弦DC的距离为:![]() ;
;
(2)由(1)得,△ODC是等边三角形,
∴∠OCD=60°,
∵∠ACB+∠ADC=180°,∠CDB+∠ADC=180°,
∴∠ACB=∠CDB,
∵∠B=∠B,
∴△ACB∽△CDB,
∴∠A=∠BCD=30°,
∴∠OCB=90°,
∴BC是⊙O的切线.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
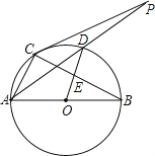
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
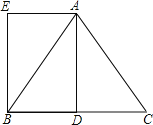
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E为BC上的点,AD平分∠BAE,CA=CD.
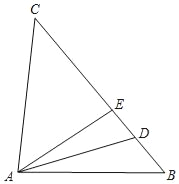
(1)求证:∠CAE=∠B;
(2)若∠B=50°,∠C=3∠DAB,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国诗词大会”带着我们“赏中华诗词、寻文化基因、品生活之美”,从古人的智慧和情怀中汲取营养、涵养心灵,其中的“飞花令”环节,在广大青少年中圈粉无数.西安铁一中分校初三二班的同学们准备在班内举行“飞花令”比赛,组织过程如下:全班同学分成五个小组,每个小组派5名同学参加比赛,这5名同学依次从写有“春”、“云”、“月”、“花”、“夜”的五张卡片中随机摸出一张(不放回),5个小组中抽取相同字的同学进行比赛(例如5名抽到“春”字同学进行以“春”为主题字的飞花令比赛).第一小组的小丽和第二小组的小英分别是各自小组第一个抽取卡片的同学.
(1)求小丽抽到“春”的概率;
(2)小丽和小英都比较擅长“春”和“月”为主题的诗句,求她们至少有一人抽到自己擅长的主题字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
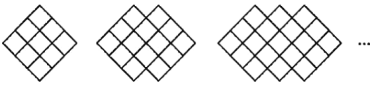
【题目】下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
A.400B.401C.402D.403
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com