
ЁОЬтФПЁПЁАжаЙњЪЋДЪДѓЛсЁБДјзХЮвУЧЁАЩЭжаЛЊЪЋДЪЁЂбАЮФЛЏЛљвђЁЂЦЗЩњЛюжЎУРЁБЃЌДгЙХШЫЕФжЧЛлКЭЧщЛГжаМГШЁгЊбјЁЂКбјаФСщЃЌЦфжаЕФЁАЗЩЛЈСюЁБЛЗНкЃЌдкЙуДѓЧрЩйФъжаШІЗлЮоЪ§ЃЎЮїАВЬњвЛжаЗжаЃГѕШ§ЖўАрЕФЭЌбЇУЧзМБИдкАрФкОйааЁАЗЩЛЈСюЁББШШќЃЌзщжЏЙ§ГЬШчЯТЃКШЋАрЭЌбЇЗжГЩЮхИіаЁзщЃЌУПИіаЁзщХЩ5УћЭЌбЇВЮМгБШШќЃЌет5УћЭЌбЇвРДЮДгаДгаЁАДКЁБЁЂЁАдЦЁБЁЂЁАдТЁБЁЂЁАЛЈЁБЁЂЁАвЙЁБЕФЮхеХПЈЦЌжаЫцЛњУўГівЛеХ(ВЛЗХЛи)ЃЌ5ИіаЁзщжаГщШЁЯрЭЌзжЕФЭЌбЇНјааБШШќ(Р§Шч5УћГщЕНЁАДКЁБзжЭЌбЇНјаавдЁАДКЁБЮЊжїЬтзжЕФЗЩЛЈСюБШШќ)ЃЎЕквЛаЁзщЕФаЁРіКЭЕкЖўаЁзщЕФаЁгЂЗжБ№ЪЧИїздаЁзщЕквЛИіГщШЁПЈЦЌЕФЭЌбЇЃЎ
ЃЈ1ЃЉЧѓаЁРіГщЕНЁАДКЁБЕФИХТЪЃЛ
ЃЈ2ЃЉаЁРіКЭаЁгЂЖМБШНЯЩУГЄЁАДКЁБКЭЁАдТЁБЮЊжїЬтЕФЪЋОфЃЌЧѓЫ§УЧжСЩйгавЛШЫГщЕНздМКЩУГЄЕФжїЬтзжЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнИХТЪЕФЖЈвхМДПЩНтОіЃЎ
ЃЈ2ЃЉЭЈЙ§БэИёСаГіЫљгаЕШПЩФмНсЙћЃЌДгжаевЕНЗћКЯЬѕМўЕФНсЙћЪ§ЃЌдйРћгУИХТЪЙЋЪНЧѓНтПЩЕУЃЎ
НтЃКЃЈ1ЃЉЁпгаЁАДКЁБЁЂЁАдЦЁБЁЂЁАдТЁБЁЂЁАЛЈЁБЁЂЁАвЙЁБЮхеХПЈЦЌЃЌ
ЁраЁРіГщЕНЁАДКЁБЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСаБэИёЕУЃК
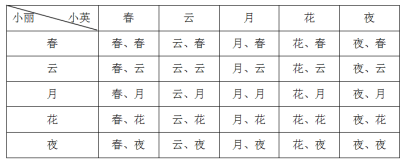
гЩБэИёПЩжЊЃЌвЛЙВга25жжЕШПЩФмЕФНсЙћЃЌЦфжаЫ§УЧжСЩйгавЛШЫГщЕНздМКЩУГЄЕФжїЬтзжЕФга16жжПЩФмЃЌЫљвдЫ§УЧжСЩйгавЛШЫГщЕНздМКЩУГЄЕФжїЬтзжЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖзїАыдВЃЌдВаФЮЊЕу
ЮЊжБОЖзїАыдВЃЌдВаФЮЊЕу![]() ЃЛвдЕу
ЃЛвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзї
ЮЊАыОЖзї![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФЦНааЯпНЛСНЛЁгкЕу
ЕФЦНааЯпНЛСНЛЁгкЕу![]() ЁЂ
ЁЂ![]() ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧЃЈ ЃЉ
ЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧЃЈ ЃЉ
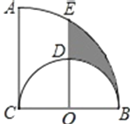
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=![]() x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ
x2+bx+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуAЃЈ0ЃЌ1ЃЉЃЌЕуBЃЈЉ9ЃЌ10ЃЉЃЌACЁЮxжсЃЌЕуPЪБжБЯпACЯТЗНХзЮяЯпЩЯЕФЖЏЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЙ§ЕуPЧвгыyжсЦНааЕФжБЯпlгыжБЯпABЁЂACЗжБ№НЛгкЕуEЁЂFЃЌЕБЫФБпаЮAECPЕФУцЛ§зюДѓЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕБЕуPЮЊХзЮяЯпЕФЖЅЕуЪБЃЌдкжБЯпACЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдCЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABCЯрЫЦЃЌШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
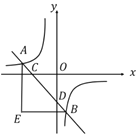
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФЕуAЃЌCдкЁбOЩЯЃЌЁбOгыABЯрНЛгкЕуDЃЌСЌНгCDЃЌЁЯAЃН30ЁуЃЌDCЃН![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓдВаФOЕНЯвDCЕФОрРыЃЛ
ЃЈ2ЃЉШєЁЯACB+ЁЯADCЃН180ЁуЃЌЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯёНЛгк
ЕФЭМЯёНЛгк![]() ЁЂ
ЁЂ![]() ЃЌгы
ЃЌгы![]() жсЁЂ
жсЁЂ![]() жсЯрНЛгк
жсЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЙ§Еу
СНЕуЃЌЙ§Еу![]() ЁЂ
ЁЂ![]() зї
зї![]() жсЁЂ
жсЁЂ![]() жсЦНааЯпНЛгкЕу
жсЦНааЯпНЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() __________ЃЎ
__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊОиаЮABCDЃЌAB=4ЃЌAD=3ЃЌЕуEЮЊБпDCЩЯВЛгыЖЫЕужиКЯЕФвЛИіЖЏЕуЃЌСЌНгBEЃЌНЋBCEбиBEЗелЕУЕНBEFЃЌСЌНгAFВЂбгГЄНЛCDгкЕуGЃЌдђЯпЖЮCGЕФзюДѓжЕЪЧ( )
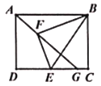
A.1B.1.5C.4-![]() D.4-
D.4-![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
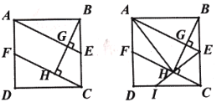
ЁОЬтФПЁПШчЭМ1ЃЌе§ЗНаЮABCDжаЃЌЕуEЪЧBCЕФжаЕуЃЌЙ§ЕуBзїBGЁЭAEгкЕуGЃЌЙ§ЕуCзїCFДЙжБBGЕФбгГЄЯпгкЕуHЃЌНЛADгкЕуF
(1)ЧѓжЄЃКЁїABGЁеЁїBCHЃЛ
(2)ШчЭМ2ЃЌСЌНгAHЃЌСЌНгEHВЂбгГЄНЛCDгкЕуIЃЛ
ЧѓжЄЃКЂй AB2=AEЁЄBHЃЛЂк Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧвЛЬЈЪЕЮяЭЖгАвЧЃЌЭМ2ЪЧЫќЕФЪОвтЭМЃЌелЯпOЉAЉBЉCБэЪОжЇМмЃЌжЇМмЕФвЛВПЗжOЉAЉBЪЧЙЬЖЈЕФЃЌСэвЛВПЗжBCЪЧПЩа§зЊЕФЃЌЯпЖЮCDБэЪОЭЖгАЬНЭЗЃЌOMБэЪОЫЎЦНзРУцЃЌAOЁЭOMЃЌДЙзуЮЊЕуOЃЌЧвAOЃН7cmЃЌЁЯBAOЃН160ЁуЃЌBCЁЮOMЃЌCDЃН8cmЃЎ
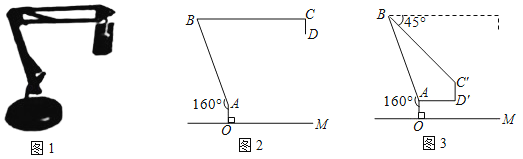
НЋЭМ2жаЕФBCШЦЕуBЯђЯТа§зЊ45ЁуЃЌЪЙЕУBCDТфдкBCЁфDЁфЕФЮЛжУЃЈШчЭМ3ЫљЪОЃЉЃЌДЫЪБCЁфDЁфЁЭOMЃЌADЁфЁЮOMЃЌADЁфЃН16cmЃЌЧѓЕуBЕНЫЎЦНзРУцOMЕФОрРыЃЌЃЈВЮПМЪ§ОнЃКsin70ЁуЁж0.94ЃЌcos70ЁуЁж0.34ЃЌcot70ЁуЁж0.36ЃЌНсЙћОЋШЗЕН1cmЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОХФъМЖФГАрзщжЏАрМЖСЊЛЖЛсЃЌзюКѓНјШыГщНБЛЗНкЃЌУПУћЭЌбЇЖМгавЛДЮГщНБЛњЛсЃЎГщНБЗНАИШчЯТЃКНЋвЛИБЦЫПЫХЦжаЕуЪ§ЮЊЁА2ЁБЁЂЁА3ЁБЁЂЁА3ЁБЁЂЁА5ЁБЁЂЁА6ЁБЕФЮхеХХЦБГУцГЏЩЯЯДдШЃЌЯШДгжаГщГі1еХХЦЃЌдйДггрЯТЕФ4еХХЦжаГщГі1еХХЦЃЌМЧТМСНеХХЦЕуЪ§КѓЗХЛиЃЌЭъГЩвЛДЮГщНБЃЎМЧУПДЮГщГіСНеХХЦЕуЪ§жЎВюЮЊ![]() ЃЌАДЯТБэвЊЧѓШЗЖЈНБЯюЃЎ
ЃЌАДЯТБэвЊЧѓШЗЖЈНБЯюЃЎ
НБЯю | вЛЕШНБ | ЖўЕШНБ | Ш§ЕШНБ |
|
|
|
|
ЃЈ1ЃЉгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЧѓГіМзЭЌбЇЛёЖўЕШНБЕФИХТЪЃЛ
ЃЈ2ЃЉХаЖЯЪЧЗёУПДЮГщНБЖМЛсЛёНБЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com