
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于
的图像交于![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴相交于
轴相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交于点
轴平行线交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
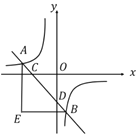
【答案】![]()
【解析】
先通过求点C、D坐标得到△COD为等腰直角三角形,进而通过△COD的面积求得一次函数关系式,再通过过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交于点
轴平行线交于点![]() 证得△AEB为等腰直角三角形,利用△AEB的面积求得AE、BE的长,设点A坐标为(m,n),表示出点B坐标,再将点A、B坐标代入反比例函数关系式得到m与n的一个方程,再把点A代入一次函数关系式,得到一个m与n的方程,联立方程组求解即可.
证得△AEB为等腰直角三角形,利用△AEB的面积求得AE、BE的长,设点A坐标为(m,n),表示出点B坐标,再将点A、B坐标代入反比例函数关系式得到m与n的一个方程,再把点A代入一次函数关系式,得到一个m与n的方程,联立方程组求解即可.
解:∵直线![]() ,
,
∴当x=0时,y=b;当y=0时,x=b,
∴C(b,0),D(0,b)
∴OC=OD=-b,
∴△COD为等腰直角三角形,∠OCD=∠ODC=45°,
∵![]() ,
,
∴![]() ,解得
,解得![]() (舍正)
(舍正)
∴直线![]() ,
,
∵过点![]() 、
、![]() 作
作![]() 轴、
轴、![]() 轴平行线交与点
轴平行线交与点![]() ,
,
∴∠EAB=∠ODC=45°,∠EBA=∠OCD=45°,
∴∠EAB=∠EBA=45°,
∴EA=EB,∠E=90°,
∵![]() ,
,
∴![]() ,解得
,解得![]() (舍负),
(舍负),
设点A为(m,n),则点B为(m+![]() ,n-
,n-![]() ),
),
将点A、B代入![]() 得
得![]() ,
,
整理得![]() ①,
①,
将点A代入![]() 得
得![]() ②,
②,
将①②联立方程组,解得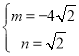 ,
,
∴![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的负半轴、
轴的负半轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限.将矩形
在第二象限.将矩形![]() 绕点
绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 落在
落在![]() 轴上,得到矩形
轴上,得到矩形![]() 与
与![]() 相交于点
相交于点![]() .若经过点
.若经过点![]() 的反比例函数
的反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() 的图象交
的图象交![]() 于点
于点![]()
![]() 则
则![]() 的长为____.
的长为____.
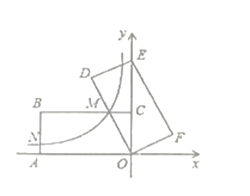
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大千故里,文化内江”,我市某中学为传承大千艺术精神,征集学生书画作品.王老师从全校20个班中随机抽取了![]() 4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
4个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
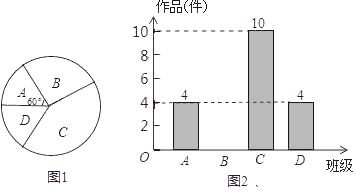
(1)王老师采取的调查方式是 (填“普查”或“抽样调査”),王老师所调查的4个班共征集到作品 件,并补全条形统计图;
(2)在扇形统计图中,表示![]() 班的扇形周心角的度数为 ;
班的扇形周心角的度数为 ;
(3)如果全校参展作品中有4件获得一等奖,其中有1名作者是男生,3名作者是女生.现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
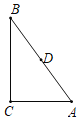
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
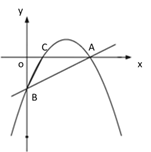
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
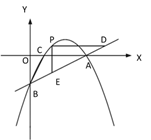
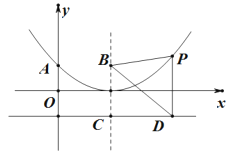
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
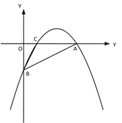
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
① ② ③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国诗词大会”带着我们“赏中华诗词、寻文化基因、品生活之美”,从古人的智慧和情怀中汲取营养、涵养心灵,其中的“飞花令”环节,在广大青少年中圈粉无数.西安铁一中分校初三二班的同学们准备在班内举行“飞花令”比赛,组织过程如下:全班同学分成五个小组,每个小组派5名同学参加比赛,这5名同学依次从写有“春”、“云”、“月”、“花”、“夜”的五张卡片中随机摸出一张(不放回),5个小组中抽取相同字的同学进行比赛(例如5名抽到“春”字同学进行以“春”为主题字的飞花令比赛).第一小组的小丽和第二小组的小英分别是各自小组第一个抽取卡片的同学.
(1)求小丽抽到“春”的概率;
(2)小丽和小英都比较擅长“春”和“月”为主题的诗句,求她们至少有一人抽到自己擅长的主题字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)如图①,若点![]() 分别为
分别为![]() 上的点,且
上的点,且![]() ,试探究
,试探究![]() 和
和![]() 的数量关系;并说明四边形
的数量关系;并说明四边形![]() 的面积是定值吗?若是,请求出;若不是,请说明理由.
的面积是定值吗?若是,请求出;若不是,请说明理由.
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且顶点在
,且顶点在![]() 轴上,与
轴上,与![]() 轴的交点为
轴的交点为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,点
,点![]() 在抛物线的对称轴上,直线
在抛物线的对称轴上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)求该抛物线的函数表达式.
(2)点![]() 是(1)中图象上的点,过点
是(1)中图象上的点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 交于点
交于点![]() .试判断
.试判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.
(3)作![]() 于点
于点![]() ,当点
,当点![]() 从横坐标2013处运动到横坐标2019处时,请求出点
从横坐标2013处运动到横坐标2019处时,请求出点![]() 运动的路径长.
运动的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com