
【题目】在10盒红色的笔芯中混放了若干支黑色的笔芯,每盒20支笔芯,每盒中混放入的黑色笔芯数如下表:
黑色笔芯数 | 0 | 1 | 4 | 5 | 6 |
盒数 | 2 | 4 | 1 | 2 | 1 |
下列结论:
①黑色笔芯一共有16支;
②从中随机取一盒,盒中红色笔芯数不低于14是必然事件;
③从中随机取一盒,盒中黑色笔芯数不超过4的概率为0.7;
④将10盒笔芯混在一起,从中随机抽取一支笔芯,恰好是黑色的概率是0.12.
其中正确的结论有()
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据表格的信息分别验证算出黑色笔芯的数量,由每盒黑色笔芯的数量可以算出每盒红色笔芯的数量,即可验证①②的正确性,再算出盒中黑色笔芯数不超过4的概率,即可判断③,用黑色的数量除以总的笔数,可验证④.
解:① 根据表格的信息,得到
黑色笔芯数=![]() ,
,
故①错误;
② 每盒笔芯的数量为20支,
∵每盒黑色笔芯的数量都≤6,
∴每盒红色笔芯≥14,
因此从中任取一盒,盒中红色笔芯数不低于14是必然事件,
故②正确;
③ 根据图表信息,得到黑色笔芯不超过4的一共有7盒,因此
从中随机取一盒,盒中黑色笔芯数不超过4的概率为7÷10=0.7
故③正确
④ 10盒笔芯一共有10×20=200(支),
由详解①知黑色笔芯共有24支,
将10盒笔芯混在一起,从中随机抽取一支笔芯,恰好是黑色的概率是24÷200=0.12,
故④正确;
综上有三个正确结论,
故答案为C.


科目:初中数学 来源: 题型:
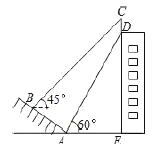
【题目】如图,某建筑物的顶部有一块标识牌![]() ,小明在斜坡上
,小明在斜坡上![]() 处测得标识牌顶部
处测得标识牌顶部![]() 的仰角为
的仰角为![]() ,沿斜坡走下来在地面
,沿斜坡走下来在地面![]() 处测得标识牌底部
处测得标识牌底部![]() 的仰角为60°,已知斜坡
的仰角为60°,已知斜坡![]() 的坡角为30°,
的坡角为30°,![]() 米. 则标识牌
米. 则标识牌![]() 的高度是米__________.
的高度是米__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
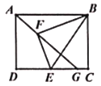
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
A.1B.1.5C.4-![]() D.4-
D.4-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
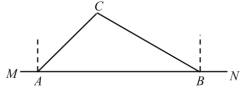
【题目】如图,某公路局施工队要修建一条东西方向的公路![]() ,已知
,已知![]() 点周围100米范围内为古建筑保护群,在
点周围100米范围内为古建筑保护群,在![]() 上的点
上的点![]() 处测得
处测得![]() 在
在![]() 的北偏东
的北偏东![]() 方向上,从
方向上,从![]() 向东走400米到达
向东走400米到达![]() 处,测得
处,测得![]() 在点
在点![]() 的北偏西
的北偏西![]() 方向上.(参考数据:
方向上.(参考数据:![]() ,
,![]() )
)
(1)![]() 是否穿过古建筑保护群?为什么?
是否穿过古建筑保护群?为什么?
(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高![]() ,则原计划完成这项工程需要多少天?
,则原计划完成这项工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
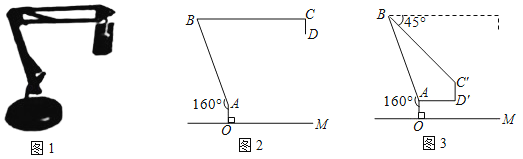
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2,图3是三张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,![]() 两点都在格点上,连结
两点都在格点上,连结![]() ,请完成下列作图:
,请完成下列作图:
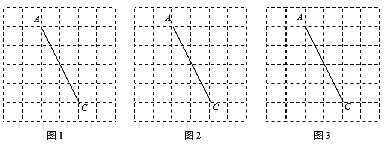
(1)以![]() 为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
为对角线在图1中作一个正方形,且正方形各顶点均在格点上.
(2)以![]() 为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
为对角线在图2中作一个矩形,使得矩形面积为6,且矩形各顶点均在格点上.
(3)以![]() 为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上.
为对角线在图3中作一个面积最小的平行四边形,且平行四边形各顶点均在格点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在C′的位置,C′D交AB于点Q,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,如果
运动,如果![]() 、
、![]() 两点同时出发,
两点同时出发,![]() 的速度为1个单位/秒.
的速度为1个单位/秒.![]() 在
在![]() 上的速度为1个单位/秒,在
上的速度为1个单位/秒,在![]() 上的速度为
上的速度为![]() 个单位/秒.设出发时间为
个单位/秒.设出发时间为![]() ,记
,记![]() 的面积
的面积![]() 的函数图象为
的函数图象为![]() .
.

(1)当![]() 时,
时,![]() 的长是_________;
的长是_________;
(2)若直线![]() 与
与![]() 有两个交点,则
有两个交点,则![]() 的取值范围为_________.
的取值范围为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
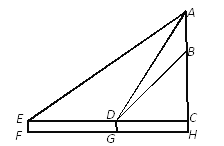
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com