
【题目】在平面直角坐标系xoy中,对于某点P(P不是原点),称以点P为圆心,![]() 长为半径圆为点P的半长圆;对于点Q,若将点P的半长圆
长为半径圆为点P的半长圆;对于点Q,若将点P的半长圆![]() 绕原点旋转,能够使得点Q位于点P的半长圆内部或圆上,则称点Q能被点P半长捕获(或点P能半长捕获点Q).
绕原点旋转,能够使得点Q位于点P的半长圆内部或圆上,则称点Q能被点P半长捕获(或点P能半长捕获点Q).
(1)在平面直角坐标系xoy中,点M(2,0),则点M的半长圆的面积为 ;下列各点![]() ,能被点M半长捕获的点有 ;
,能被点M半长捕获的点有 ;
(2)已知点![]() ,
,
①点N(0,n),当t=1时,线段EF上的所有点均可以被点N半长捕获,求n的取值范围;
②若对于平面上的任意点(原点除外)都不能半长捕获线段EF上的所有点,直接写出t的取值范围.
【答案】(1)![]() ,B点和C点;(2)①
,B点和C点;(2)①![]() 或
或![]() ;②
;②![]() .
.
【解析】
(1)根据M点坐标,先求出M的半长圆的半径,由此可求面积,再根据题述定义,画出大致图,由图可知被点M半长捕获的点到原点的距离介于1到3之间,分别计算出各点到圆心的距离,即可得出被点M半长捕获的点;
(2)①当n>0时,根据题述定义可得被点N半长捕获的点到原点的距离介于![]() 到
到![]() 之间,由此可列出不等式组,即可求得n的取值范围,同理可求得n<0时,n的取值范围;
之间,由此可列出不等式组,即可求得n的取值范围,同理可求得n<0时,n的取值范围;
②设半长圆![]() 的半径为r,则被点N半长捕获的点到原点的距离介于r到3r之间,根据题意,可列出关于r的不等式组,且该不等式组无解,即可求得t的取值范围.
的半径为r,则被点N半长捕获的点到原点的距离介于r到3r之间,根据题意,可列出关于r的不等式组,且该不等式组无解,即可求得t的取值范围.
解:(1)如下图,
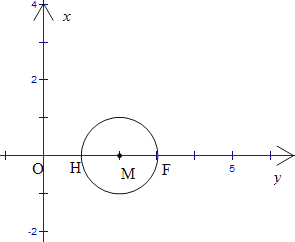
∵M(2,0),
∴过M点的半长圆半径为1,即HM=MF=1,
∴OH=1,OF=3,![]() ,
,
∴被点M半长捕获的点到原点的距离介于1到3之间,
又∵![]() ,
,
∴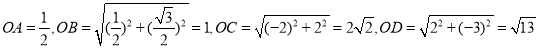 ,
,
所以,能被点M半长捕获的点有B点和C点.
故答案为:![]() ,B点和C点;
,B点和C点;
(2)①根据点N(0,n),
若n>0,则半长圆![]() 的半径为
的半径为![]() ,
,
此时,被点N半长捕获的点到原点的距离介于![]() 到
到![]() 之间,
之间,
∵![]() 且
且![]() ,
,
∴![]() ,
,
又∵线段EF上的所有点均可以被点N半长捕获,
∴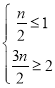 ,解得
,解得![]() ,
,
若n<0,同理可得![]() ,
,
故![]() 或
或![]() ;
;
②∵![]() ,
,
∴![]() ,
,
设半长圆![]() 的半径为r,
的半径为r,
则被点N半长捕获的点到原点的距离介于r到3r之间,
若对于平面上的任意点(原点除外)都不能半长捕获线段EF上的所有点,则
关于r的不等式组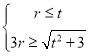 无解,
无解,
即![]() ,解得
,解得![]() ,
,
又∵![]() ,
,
∴![]() ,
,


科目:初中数学 来源: 题型:
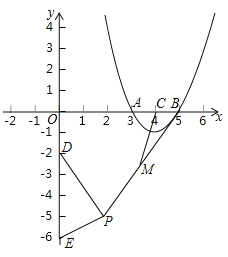
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,对称轴与
两点,对称轴与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 是平面内一动点,且满足
是平面内一动点,且满足![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________________.
的最大值是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为国家级开发区的两江新区,大小公园星罗棋布,称为“百园之城”.该区2018年绿地总面积为2500万平方米,2020年绿地总面积将比2018年增加3500万平方米,人口比2018年增加50万人.这样,2020年该区人均绿地面积是2018年人均绿地面积的2倍.
(1)求2020年两江新区的人口数量;
(2)2020年起,为了更好地建设“一半山水一半城”的美丽新区,吸引外来人才落户两江新区,新区管委会在增加绿地面积的同时大力扩展配套水域面积.根据调查,2020年新区的配套水域面积为人均4平方米.在2020年的基础上,如果人均绿地每增加1平方米,人均配套水域将增加![]() 平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
平方米,人口也将随之增加5万.这样,两江新区2022年的绿地总面积与配套水域总面积要在2020年的基础上增加75%,那么2022年人均绿地面积要比2020年增加多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
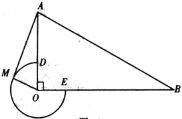
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
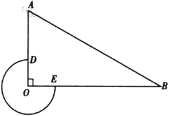
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个倾斜角为![]() 的斜坡的横截面,
的斜坡的横截面,![]() .斜坡顶端B与地面的距离
.斜坡顶端B与地面的距离![]() 为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系
为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系![]() (a,b是常数,
(a,b是常数,![]() ),图2记录了x与y的相关数据.
),图2记录了x与y的相关数据.
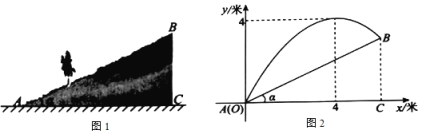
(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.8米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:![]() 品格健全,成绩优异;
品格健全,成绩优异;![]() 尊敬师长,积极进取;
尊敬师长,积极进取;![]() 自控力差,被动学习;
自控力差,被动学习;![]() 沉迷奢玩,消极自卑.
沉迷奢玩,消极自卑.
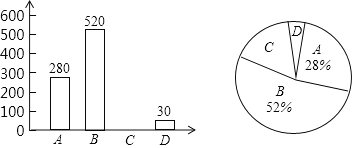
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中![]() 类所在扇形的圆心角为 度;
类所在扇形的圆心角为 度;
(4)东至县城内某中学有在校学生3330人,请估算该校![]() 类学生人数.
类学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知矩形ABCD,AB=4,AD=3,点E为边DC上不与端点重合的一个动点,连接BE,将BCE沿BE翻折得到BEF,连接AF并延长交CD于点G,则线段CG的最大值是( )
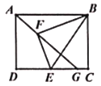
A.1B.1.5C.4-![]() D.4-
D.4-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
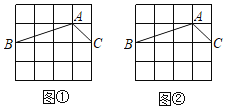
【题目】图①、图②都是![]() 的正方形网格,每个小正方形的顶点叫做格点.
的正方形网格,每个小正方形的顶点叫做格点.![]() 的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
的顶点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中过点![]() 作
作![]() 面积两等分的射线.
面积两等分的射线.
(2)在图②中过点![]() 作所有将
作所有将![]() 面积分成1:2的两部分的射线.
面积分成1:2的两部分的射线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com