
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
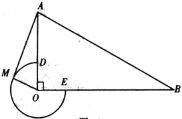
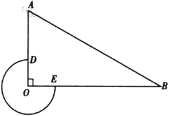
备用图
【答案】(1)AM与优弧的相切(2)![]() 或
或![]() (3)
(3)![]()
【解析】
(1)根据勾股定理的得到∠AMO=90°即可得到![]() 与优弧
与优弧![]() 的相切;
的相切;
(2)根据题意分![]() 在直线
在直线![]() 的左侧和右侧两种情况讨论,用三角函数及相似三角形的性质进行求解;(3)根据题意作过点
的左侧和右侧两种情况讨论,用三角函数及相似三角形的性质进行求解;(3)根据题意作过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 此时
此时![]() 的面积最大,过点
的面积最大,过点![]() 作
作![]() 于点
于点![]() ,即点
,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() 的面积最小,分别求出
的面积最小,分别求出![]() 最大值与最小值即可求解.
最大值与最小值即可求解.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() .
.
(1)![]() 与优弧的相切;
与优弧的相切;
如图1,当![]() 时,
时,![]() ,
,![]() 且
且![]()
![]() 为直角三角形,
为直角三角形,![]() ,
,
![]() 点
点![]() 在
在![]() 上,
上,![]()
![]() 与优弧
与优弧![]() 的相切.
的相切.
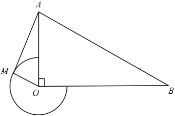
(2)当![]() 时,第一种情况:如图 2所示,
时,第一种情况:如图 2所示,![]() 在直线
在直线![]() 的左侧;
的左侧;![]()
![]()
过点![]() 作
作![]() 于点
于点![]()
在![]() 中,
中,![]()
![]() ,
,![]() ,
,![]()
在![]() 中,据勾股定理可知
中,据勾股定理可知![]() .
.
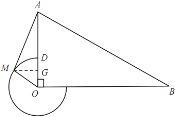
第二种情况:如图 3所示,![]() 在直线
在直线![]() 的右侧;连接
的右侧;连接![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,据勾股定理得:
中,据勾股定理得:![]()
由![]() 可知
可知![]() .
.

(3)如图4,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() 此时
此时![]() 的面积最大
的面积最大
在![]() 中,
中,![]() ,
,![]()
![]()
![]()
在![]() 中
中![]()
![]()
![]()
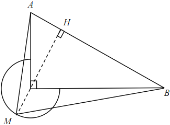
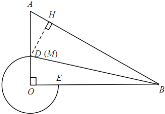
如图5,过点![]() 作
作![]() 于点
于点![]() ,即点
,即点![]() 与点
与点![]() 重合,此时
重合,此时![]() 的面积最小
的面积最小
在![]() 中
中
![]()
![]()
![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:

(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )

A、9:4 B、3:2 C、![]() :
:![]() D、3
D、3![]() :2
:2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 坐标是
坐标是![]() .当把坐标系绕点
.当把坐标系绕点![]() 顺时针选择30°时,点
顺时针选择30°时,点![]() 在旋转后的坐标系中的坐标是____;当把坐标系绕点
在旋转后的坐标系中的坐标是____;当把坐标系绕点![]() 逆时针选择30°时,点
逆时针选择30°时,点![]() 在旋转后的坐标系中的坐标是____.
在旋转后的坐标系中的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
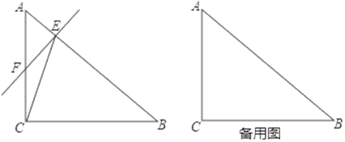
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点E从点A出发沿着线段AB向终点B运动,速度为每秒3个单位长度,过点E作EF⊥AB交直线AC于点F,连结CE.设点E的运动时间为t秒.
(1)当点F在线段AC上(不含端点)时,
①求证:△ABC∽△AFE;
②当t为何值时,△CEF的面积为1.2;
(2)在运动过程中,是否存在某时刻t,使△CEF为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
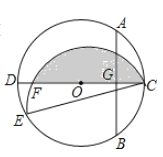
【题目】如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为G,OG:OC=3:5,AB=8.点E为圆上一点,∠ECD=15°,将![]() 沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
沿弦CE翻折,交CD于点F,图中阴影部分的面积=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
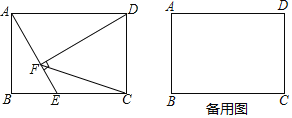
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com