
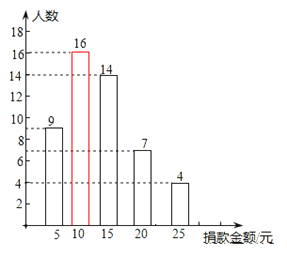
【题目】“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:

(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
【答案】(1)该班的总人数为50(人);
(2)捐款10元的人数 16人,图见解析;
(3)该班平均每人捐款13.1元.
【解析】
(1)根据频数、频率和总量的关系,用捐款15元的人数14除以所占的百分比28%,计算即可得解.
(2)用该班总人数减去其它四种捐款额的人数,计算即可求出捐款10元的人数,然后补全条形统计图,根据众数的定义,人数最多即为捐款总额的众数.
(3)根据加权平均数的求解方法列式计算即可得解.
解:(1)该班的总人数为14÷28%=50(人).
(2)捐款10元的人数:50﹣9﹣14﹣7﹣4=50﹣34=16.
图形补充如下图所示,众数是10:
(3)∵![]() (5×9+10×16+15×14+20×7+25×4)=
(5×9+10×16+15×14+20×7+25×4)=![]() ×655=13.1(元),
×655=13.1(元),
∴该班平均每人捐款13.1元.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标(0,6),AC⊥y轴,且AC=AO,点B,C横坐标相同,点D在AC上,tan∠AOD=![]() ,若反比例函数y=
,若反比例函数y=![]() (x>0)的图象经过点B、D.
(x>0)的图象经过点B、D.
(1)求:k及点B坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点A1的坐标是A1(m,n),求:代数式m+3n的值以及点A1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD =∠BCE = 90°,点M为AN的中点,过点E与AD平行的直线交射线AM于点N。

(1)当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,PB是⊙O的切线,B为切点,圆心O在PC上,∠P=30°,D为弧BC的中点.
(1)求证:PB=BC;
(2)试判断四边形BOCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试探究∠BAD与∠CDE的数量关系;
(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其它条件不变,试继续探究∠BAD与∠CDE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为正方形,E是BC的中点,连接AE,过点A作∠AFD,使∠AFD=2∠EAB,AF交CD于点F,如图①,易证:AF=CD+CF.
(1)如图②,当四边形ABCD为矩形时,其他条件不变,线段AF,CD,CF之间有怎样的数量关系?请写出你的猜想,并给予证明;
(2)如图③,当四边形ABCD为平行四边形时,其他条件不变,线段AF,CD,CF之间又有怎样的数量关系?请直接写出你的猜想.
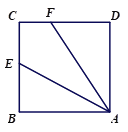
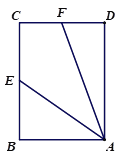
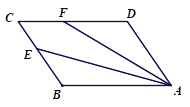
图① 图② 图③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com