
【题目】探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试探究∠BAD与∠CDE的数量关系;
(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其它条件不变,试继续探究∠BAD与∠CDE的数量关系.

【答案】(1)∠EDC=30°;(2)∠EDC=![]() ∠BAD,证明见解析;(3)∠EDC=
∠BAD,证明见解析;(3)∠EDC=![]() ∠BAD,证明见解析.
∠BAD,证明见解析.
【解析】
(1)先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+60°=105°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论;
(2)(3)利用(1)的思路与方法解答即可.
(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=105°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC﹣∠EDC=105°﹣∠EDC=45°+∠EDC,
解得:∠EDC=30°.
(2)∠EDC=![]() ∠BAD.
∠BAD.
证明:设∠BAD=x,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=45°+x,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC﹣∠EDC=∠45°+x﹣∠EDC=45°+∠EDC,
解得:∠EDC=![]() ∠BAD.
∠BAD.
(3)∠EDC=![]() ∠BAD.
∠BAD.
证明:设∠BAD=x,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠B+x,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC﹣∠EDC=∠B+x﹣∠EDC=∠B+∠EDC,
解得:∠EDC=![]() ∠BAD.
∠BAD.


科目:初中数学 来源: 题型:
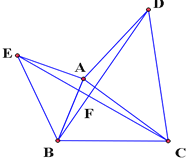
【题目】如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.
(1)求证:∠BDA=∠ECA.
(2)若m=![]() ,n=3,∠ABC=75°,求BD的长.
,n=3,∠ABC=75°,求BD的长.
(3)当∠ABC=____时,BD最大,最大值为____(用含m,n的代数式表示)
(4)试探究线段BF,AE,EF三者之间的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:

(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级![]() 班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
班同学小明和小亮,升入九年级时学校采用随机的方式编班,已知九年级共分六个班,小明和小亮被分在同一个班的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC内一点D,点C是AE上一点,AD交BE于点P,射线DC交BE的延长线于点F,且∠ABD=∠ACD,∠PDB=∠PDC
(1)求证:AB=AC;
(2)若AB=3,AE=5,求![]() 的值;
的值;
(3)若![]() ,
,![]() =m,则
=m,则![]() =_______.
=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.

(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,甲、乙两车从![]() 地出发,沿相同路线前往同一目的地,途中经过
地出发,沿相同路线前往同一目的地,途中经过![]() 地.甲车先出发,当甲车到达
地.甲车先出发,当甲车到达![]() 地时,乙车开始出发.当乙车到达
地时,乙车开始出发.当乙车到达![]() 地时,甲车与
地时,甲车与![]() 地相距
地相距![]() .设甲、乙两车与
.设甲、乙两车与![]() 地之间的距离为,
地之间的距离为,![]() ,
,![]() ,乙车行驶的时间为
,乙车行驶的时间为![]() ,
,![]() ,
,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
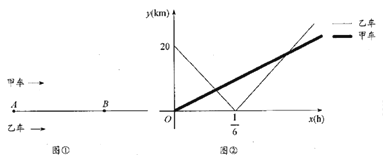
(1)![]() ,
,![]() 两地之间的距离为
两地之间的距离为 ![]() ;
;
(2)当![]() 为何值时,甲、乙两车相距
为何值时,甲、乙两车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两地之间有一条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF(EF=DC),可直接沿直线AB从A地到达B地,已知BC=12km,∠A=45°,∠B=30°,桥DC和AB平行.
(1)求桥DC与直线AB的距离;
(2)现在从A地到达B地可比原来少走多少路程?
(以上两问中的结果均精确到0.1km,参考数据:![]() ≈1.14,
≈1.14,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com