Question

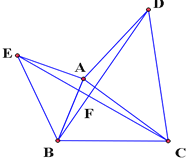
【题目】如图，已知△ABC，分别以AB,AC为直角边，向外作等腰直角三角形ABE和等腰直角三角形ACD，∠EAB=∠DAC=90°，连结BD,CE交于点F，设AB=m，BC=n.

（1）求证：∠BDA=∠ECA.

（2）若m=，n=3，∠ABC=75°，求BD的长.

（3）当∠ABC=____时，BD最大，最大值为____（用含m，n的代数式表示）

（4）试探究线段BF,AE,EF三者之间的数量关系。

Answer 1

【答案】135° m+n

【解析】

试题

（1）由已知条件证△ABD≌△AEC，即可得到∠BDA=∠CEA；

（2）过点E作EG⊥CB交CB的延长线于点G，由已知条件易得∠EBG=60°，BE=2，这样在Rt△BEG中可得EG=，BG=1，结合BC=n=3，可得GC=4，由长可得EC=，结合△ABD≌△AEC可得BD=EC=；

（3）由（2）可知，BE=，BC=n，因此当E、B、C三点共线时，EC最大=BE+BC=，此时BD最大=EC最大=；

（4）由△ABD≌△AEC可得∠AEC=∠ABD，结合△ABE是等腰直角三角形可得△EFB是直角三角形及BE2=2AE2，从而可得EF2=BE2-BF2=2AE2-BF2.

试题解析：

（1）∵△ABE和△ACD都是等腰直角三角形，且∠EAB=∠DAC=90°，

∴AE=AB，AC=AD，∠EAB+∠BAC=∠BAC+∠DAC，即∠EAC=∠BAD，

∴△EAC≌△BAD，

∴∠BDA=∠ECA；

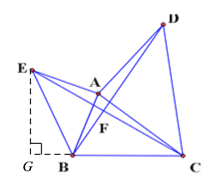
（2）如下图，过点E作EG⊥CB交CB的延长线于点G，

∴∠EGB=90°，

∵在等腰直角△ABE，∠BAE=90°，AB=m= ，

∴∠ABE=45°，BE=2，

∵∠ABC=75°，

∴∠EBG=180°-75°-45°=60°，

∴BG=1，EG=，

∴GC=BG+BC=4，

∴CE=，

∵△EAC≌△BAD，

∴BD=EC=；

（3）由（2）可知，BE=，BC=n，因此当E、B、C三点共线时，EC最大=BE+BC=，

∵BD=EC，

∴BD最大=EC最大=，此时∠ABC=180°-∠ABE=180°-45°=135°，

即当∠ABC=135°时，BD最大=；

（4）∵△ABD≌△AEC，

∴∠AEC=∠ABD，

∵在等腰直角△ABE中，∠AEC+∠CEB+∠ABE=90°，

∴∠ABD+∠ABE+∠CEB=90°，

∴∠BFE=180°-90°=90°，

∴EF2+BF2=BE2，

又∵在等腰Rt△ABE中，BE2=2AE2，

∴2AE2=EF2+BF2.