
【题目】如图,△ABC中,∠ACB=90°,AC<BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

【答案】30°
【解析】
先确定△CDF是等腰三角形,得出∠CFD=∠CDF=45°,因为不确定△BDE是以那两条边为腰的等腰三角形,故需讨论,①DE=DB,②BD=BE,③DE=BE,然后分别利用角的关系得出答案即可.
解:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=![]() ∠CFD=22.5°,∠DEB=2x°,
∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,如图1所示:
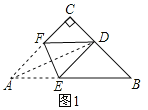
∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.
此时∠B=2x=45°,
∵AC<BC,
∴∠B=45°不成立;
②当BD=BE时,如图2所示:
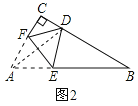
则∠B=(180°﹣4x)°,∠CAD=22.5°.
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,
此时∠B=(180﹣4x)°=30°.
③DE=BE时,则∠B=![]() (180﹣2x)°,
(180﹣2x)°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+![]() (180﹣2x)°,
(180﹣2x)°,
此方程无解.
∴DE=BE不成立.
综上所述,∠B=30°.
故答案为:30°.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴,y轴分别交于B,C两点,抛物线
与x轴,y轴分别交于B,C两点,抛物线![]() 过点B,C.
过点B,C.
(1)求b、c的值;
(2)若点D是抛物线在x轴下方图象上的动点,过点D作x轴的垂线,与直线BC相交于点E.当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
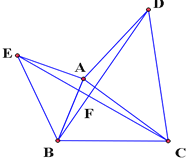
【题目】如图,已知△ABC,分别以AB,AC为直角边,向外作等腰直角三角形ABE和等腰直角三角形ACD,∠EAB=∠DAC=90°,连结BD,CE交于点F,设AB=m,BC=n.
(1)求证:∠BDA=∠ECA.
(2)若m=![]() ,n=3,∠ABC=75°,求BD的长.
,n=3,∠ABC=75°,求BD的长.
(3)当∠ABC=____时,BD最大,最大值为____(用含m,n的代数式表示)
(4)试探究线段BF,AE,EF三者之间的数量关系。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com