
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
【答案】(1)排球50元,篮球80元;(2)①y=-30m+4800 ;m=34、35、36、37、38; ②排球38个,篮球22个时,费用最低为3660.
【解析】
设每个排球需要x元,每个篮球的价格是y元,根据题意列出方程组![]() ,解方程组即可求解;(2)①设购买排球m个,则购买篮球(60-m)个,根据“一次性购买排球和篮球共60个,总费用不超过3 800元”不等式组,解不等式组求得m的取值范围,再结合买排球的个数少于39个即可求得m的具体数值;根据“买排球的总费用+买篮球的总费用=y”即可求得y关于m的函数关系式;②根据排球比较便宜,可知购买排球越多,总费用越低,由此即可解答.
,解方程组即可求解;(2)①设购买排球m个,则购买篮球(60-m)个,根据“一次性购买排球和篮球共60个,总费用不超过3 800元”不等式组,解不等式组求得m的取值范围,再结合买排球的个数少于39个即可求得m的具体数值;根据“买排球的总费用+买篮球的总费用=y”即可求得y关于m的函数关系式;②根据排球比较便宜,可知购买排球越多,总费用越低,由此即可解答.
(1)设每个排球需要x元,每个篮球的价格是y元,
由题意得:![]() ,
,
解得: ![]() ,
,
∴购买一个排球的价格是50元,每个篮球的价格为80元.
(2)①设购买排球m个,则购买篮球(60-m)个,由题意得:
50m+80(60-m)≤3800,
解得m≥![]() ;
;
∵排球的个数少于39个,
∴m<39,
∴排球的个数可以为34,35,36,37,38.
∵总费用为y元,
∴y=50m+80(60-m)=-30m+4800.
②∵排球比较便宜,
∴购买排球越多,总费用越低,
∴当购买排球38个,篮球22个时,费用最低,此时的费用为38×50+22×80=1900+1760=3660(元).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C和坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
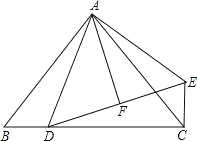
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=![]() x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________
x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O ![]() C
C ![]() B
B ![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.

(1)当t=2时,求直线PD的解析式。
(2)当P在BC上,OP+PD有最小值时,求点P的坐标。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=﹣x﹣b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x﹣k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),将点O , A , B , C的横坐标、纵坐标都乘以-2.
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件:①∠A+∠B=∠C,②∠A∶∠B∶∠C=3∶4∶5,③∠C=∠A-∠B, ④a∶b∶c=3∶4∶5 中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com