
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),将点O , A , B , C的横坐标、纵坐标都乘以-2.
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比.
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣ ![]() )
)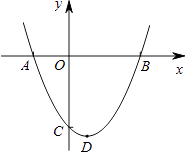
(1)求抛物线对应的函数关系式;
(2)求四边形ACDB的面积;
(3)若平移(1)中的抛物线,使平移后的抛物线与坐标轴仅有两个交点,请直接写出一个平移后的抛物线的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划一次性购买排球和篮球,每个篮球的价格比排球贵30元;购买2个排球和3个篮球共需340元.
(1)求每个排球和篮球的价格:
(2)若该校一次性购买排球和篮球共60个,总费用不超过3800元,且购买排球的个数少于39个.设排球的个数为m,总费用为y元.
①求y关于m的函数关系式,并求m可取的所有值;
②在学校按怎样的方案购买时,费用最低?最低费用为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上画出点P,使PB+PC最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
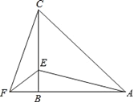
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=25°,求∠BFC度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB , 垂足为D , AB=c , ∠a=α , 则CD长为( ) 
A.csin2α
B.ccos2α
C.csinαtanα
D.csinαcosα
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中CD的长是(结果精确到0.1)(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)( )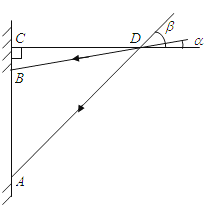
A.1.2米
B.1.5米
C.1.9米
D.2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com