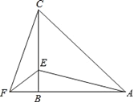
【题目】在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF．

（1）求证：△ABE≌△CBF；

（2）若∠CAE＝25°，求∠BFC度数．

参考答案：

【答案】

【1】 证明：∵∠ABC＝90°，∴∠CBF＝∠ABE＝90°.

在Rt△ABE和Rt△CBF中，

∵AE＝CF, AB＝BC，

∴Rt△ABE≌Rt△CBF(HL)．---------------------4分

【2】 解：∵AB＝BC, ∠ABC＝90°，

∴∠CAB＝∠ACB＝45°.

∵∠BAE＝∠CAB－∠CAE＝45°－25°＝20°，

由(1)得Rt△ABE≌Rt△CBF，

∴∠BCF＝∠BAE＝20°，

∴∠ACF＝∠BCF＋∠ACB＝45°＋20°＝65°. ---------------------8分

【解析】

（1）由AB=CB，∠ABC=90°，AE=CF，即可利用HL证得Rt△ABE≌Rt△CBF；

（2）由AB=CB，∠ABC=90°，即可求得∠CAB与∠ACB的度数，即可得∠BAE的度数，又由Rt△ABE≌Rt△CBF，即可求得∠BCF的度数，则由∠ACF=∠BCF+∠ACB即可求得答案.

关闭