[题目]如图.某沿海城市A接到台风警报.在该城市正南方向260 km的B处有一台风中心.沿BC方向以15 km/h的速度向C移动.已知城市A到BC的距离AD＝100 km.那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响.正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，某沿海城市A接到台风警报，在该城市正南方向260 km的B处有一台风中心，沿BC方向以15 km/h的速度向C移动，已知城市A到BC的距离AD＝100 km，那么台风中心经过多长时间从B点移动到D点？如果在距台风中心30 km的圆形区域内都将受到台风的影响，正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响？

【答案】在接到台风警报后的14 h内撤离才可以免受台风的影响．

【解析】

首先根据勾股定理计算BD的长，再根据时间=路程÷速度计算从B点移动到D点所用时间；根据在30千米范围内都要受到影响，先求出从点B到受影响的距离与结束影响的距离，再根据时间=路程÷速度计算，然后求出时间段即可．

根据题意，画图得：

在Rt△ABD中，∵AB＝260 km，AD＝100 km，

∴台风中心从B点移动到D点所用的时间为

在D点休息的游人应在台风中心距D点30 km前撤离，30÷15＝2(h)，16－2＝14(h)．

答：在接到台风警报后的14 h内撤离才可以免受台风的影响．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】已知关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根．
（1）求k的取值范围；
（2）若k为正整数，求该方程的根．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，直线AB：y=﹣x﹣b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．

（1）求点B的坐标；
（2）求直线BC的解析式；
（3）直线EF：y=2x﹣k（k≠0）交AB于E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S△EBD=S△FBD？若存在，求出k的值；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

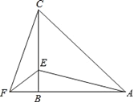
【题目】在△ABC中，AB＝CB，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF．

（1）求证：△ABE≌△CBF；

（2）若∠CAE＝25°，求∠BFC度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.

（1）画出位似中心点O；
（2）直接写出△ABC与△A′B′C′的位似比；
（3）以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点O中心对称的△A″B″C″，并直接写出△A″B″C″各顶点的坐标.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在课题学习后，同学们为教室窗户设计一个遮阳蓬，小明同学绘制的设计图如图所示，其中，AB表示窗户，且AB=2.82米，△BCD表示直角遮阳蓬，已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18°，最大夹角β为66°，根据以上数据，计算出遮阳蓬中CD的长是（结果精确到0.1）（参考数据：sin18°≈0.31，tan18°≈0.32，sin66°≈0.91，tan66°≈2.2）（　　）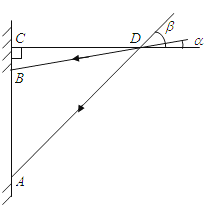

A.1.2米
B.1.5米
C.1.9米
D.2.5米