
【题目】已知关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若k为正整数,求该方程的根.
【答案】
(1)解:∵关于x的一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根,
∴△>0,
∴△=22﹣4(2k﹣2)=4﹣8k+8=12﹣8k,
∴12﹣8k>0,
∴k< ![]()
(2)解:∵k< ![]() ,并且k为正整数,
,并且k为正整数,
∴k=1,
∴该方程为x2+2x=0,
∴该方程的根为x1=0,x2=﹣2
【解析】(1)根据一元二次方程x2+2x+2k﹣2=0有两个不相等的实数根可得△=22﹣4(2k﹣2)=4﹣8k+8=12﹣8k>0,求出k的取值范围即可;(2)根据k的取值范围,结合k为正整数,得到k的值,进而求出方程的根.
【考点精析】掌握求根公式是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n﹣ ![]() ≤x<n+
≤x<n+ ![]() ,则<x>=n. 如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
,则<x>=n. 如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①<π>=________;②如果<2x﹣1>=3,则实数x的取值范围为________;
(2)①当x≥0,m为非负整数时,求证:<x+m>=m+<x>;②举例说明<x+y>=<x>+<y>不恒成立;
(3)求满足<x>= ![]() x的所有非负实数x的值.
x的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费![]() (元)与用水量
(元)与用水量![]() (吨)的函数关系如图所示。
(吨)的函数关系如图所示。
(1)分别写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
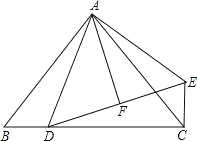
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=![]() x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________
x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海城市A接到台风警报,在该城市正南方向260 km的B处有一台风中心,沿BC方向以15 km/h的速度向C移动,已知城市A到BC的距离AD=100 km,那么台风中心经过多长时间从B点移动到D点?如果在距台风中心30 km的圆形区域内都将受到台风的影响,正在D点休息的游人在接到台风警报后的几小时内撤离才可以免受台风的影响?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com