
ЁОЬтФПЁПЖдЗЧИКЪЕЪ§xЁАЫФЩсЮхШыЁБЕНИіЮЛЕФжЕМЧЮЊЃМxЃОЃЌМДЃКЕБnЮЊЗЧИКећЪ§ЪБЃЌШчЙћnЉ ![]() ЁмxЃМn+
ЁмxЃМn+ ![]() ЃЌдђЃМxЃО=nЃЎ ШчЃКЃМ0ЃО=ЃМ0.48ЃО=0ЃЌЃМ0.64ЃО=ЃМ1.493ЃО=1ЃЌЃМ2ЃО=2ЃЌЃМ3.5ЃО=ЃМ4.12ЃО=4ЃЌЁ
ЃЌдђЃМxЃО=nЃЎ ШчЃКЃМ0ЃО=ЃМ0.48ЃО=0ЃЌЃМ0.64ЃО=ЃМ1.493ЃО=1ЃЌЃМ2ЃО=2ЃЌЃМ3.5ЃО=ЃМ4.12ЃО=4ЃЌЁ
ЪдНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЬюПеЃКЂйЃМІаЃО=________ЃЛЂкШчЙћЃМ2xЉ1ЃО=3ЃЌдђЪЕЪ§xЕФШЁжЕЗЖЮЇЮЊ________ЃЛ
ЃЈ2ЃЉЂйЕБxЁн0ЃЌmЮЊЗЧИКећЪ§ЪБЃЌЧѓжЄЃКЃМx+mЃО=m+ЃМxЃОЃЛЂкОйР§ЫЕУїЃМx+yЃО=ЃМxЃО+ЃМyЃОВЛКуГЩСЂЃЛ
ЃЈ3ЃЉЧѓТњзуЃМxЃО= ![]() xЕФЫљгаЗЧИКЪЕЪ§xЕФжЕЃЎ
xЕФЫљгаЗЧИКЪЕЪ§xЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ3ЃЛ![]() ЁмxЃМ
ЁмxЃМ ![]() ;(2)МћНтЮіЃЛЃЈ3ЃЉ3ЃЛ
;(2)МћНтЮіЃЛЃЈ3ЃЉ3ЃЛ![]() ЁмxЃМ
ЁмxЃМ ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉІаЕФЪЎЗжЮЛЮЊ1ЃЌгІИУЩсШЅЃЌЫљвдОЋШЗЕНИіЮЛЪЧ3ЃЛШчЙћОЋШЗЪ§ЪЧ3ЃЌФЧУДетИіЪ§гІИУдк2.5КЭ3.5жЎМфЃЌАќРЈ2.5ЃЌВЛАќРЈ3.5ЃЌШУ2.5Ём2xЃ1ЃМ3.5ЃЌНтВЛЕШЪНМДПЩЃЛЃЈ2ЃЉЂйЗжБ№БэЪОГі<xЃЋm>КЭ<x>ЃЌМДПЩЕУЕНЫљЧѓВЛЕШЪНЃЛЂкОйГіЗДР§ЫЕУїМДПЩЃЌЦЉШчЩдЮЂГЌЙ§0.5ЕФСНИіЪ§ЯрМгЃЛЃЈ3ЃЉ![]() xЮЊећЪ§ЃЌЩшетИіећЪ§ЮЊkЃЌвзЕУетИіећЪ§гІдкkЃ
xЮЊећЪ§ЃЌЩшетИіећЪ§ЮЊkЃЌвзЕУетИіећЪ§гІдкkЃ![]() КЭkЃЋ
КЭkЃЋ![]() жЎМфЃЌАќРЈkЃ
жЎМфЃЌАќРЈkЃ![]() ЃЌВЛАќРЈkЃЋ
ЃЌВЛАќРЈkЃЋ![]() ЃЌЧѓЕУећЪ§kЕФжЕМДПЩЧѓЕУxЕФЗЧИКЪЕЪ§ЕФжЕ.
ЃЌЧѓЕУећЪ§kЕФжЕМДПЩЧѓЕУxЕФЗЧИКЪЕЪ§ЕФжЕ.
ЃЈ1ЃЉ3ЃЛ![]() ЁмxЃМ
ЁмxЃМ![]()
ЃЈ2ЃЉНтЃКЂйжЄУїЃКЩшЃМxЃО=nЃЌдђnЉ![]() ЁмxЃМn+
ЁмxЃМn+![]() ЃЌnЮЊЗЧИКећЪ§ЃЛ ЁрЃЈn+mЃЉЉ
ЃЌnЮЊЗЧИКећЪ§ЃЛ ЁрЃЈn+mЃЉЉ![]() Ёмx+mЃМЃЈn+mЃЉ+
Ёмx+mЃМЃЈn+mЃЉ+ ![]() ЃЌЧвn+mЮЊЗЧИКећЪ§ЃЌ
ЃЌЧвn+mЮЊЗЧИКећЪ§ЃЌ
ЁрЃМx+mЃО=n+m=m+ЃМxЃОЃЎ
ЂкОйЗДР§ЃКЃМ0.6ЃО+ЃМ0.7ЃО=1+1=2ЃЌЖјЃМ0.6+0.7ЃО=ЃМ1.3ЃО=1ЃЌ
ЁрЃМ0.6ЃО+ЃМ0.7ЃОЁйЃМ0.6+0.7ЃОЃЌ
ЁрЃМx+yЃО=ЃМxЃО+ЃМyЃОВЛвЛЖЈГЩСЂЃЛ
ЃЈ3ЃЉНтЃКЁпxЁн0ЃЌ ![]() xЮЊећЪ§ЃЌ Щш
xЮЊећЪ§ЃЌ Щш ![]() x=kЃЌkЮЊећЪ§ЃЌ
x=kЃЌkЮЊећЪ§ЃЌ
дђx= ![]() kЃЌ
kЃЌ
ЁрЃМ![]() kЃО=kЃЌ
kЃО=kЃЌ
ЁрkЉ![]() Ём
Ём![]() kЃМk+
kЃМk+![]() ЃЌkЁн0ЃЌ
ЃЌkЁн0ЃЌ
Ёп0ЁмkЁм2ЃЌ
Ёрk=0ЃЌ1ЃЌ2ЃЌ
Ёрx=0ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК3ЃЛ ![]() ЁмxЃМ
ЁмxЃМ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
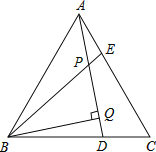
ЁОЬтФПЁПШчЭМЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌAE=CDЃЌADЁЂBEЯрНЛгкЕуPЃЌBQЁЭADгкQЃЎ
(1ЃЉЧѓжЄЃКЁїADCЁеЁїBEAЃЛ
ЃЈ2ЃЉШєPQ=4ЃЌPE=1ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФШ§ИіЖЅЕудкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжаЃЌвбжЊAЃЈЉ1ЃЌЉ1ЃЉЃЌBЃЈ4ЃЌЉ1ЃЉЃЌCЃЈ3ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЛГіЁїABCЙигкyжсЖдГЦЕФЁїAЁфBЁфCЁфЃЈЦфжаAЁфЃЌBЁфЃЌCЁфЗжБ№ЪЧAЃЌBЃЌCЕФЖдгІЕуЃЌВЛаДЛЗЈЃЉЃЛ
ЃЈ2ЃЉЗжБ№аДГіAЁфЃЌBЁфЃЌCЁфШ§ЕуЕФзјБъЃЛ
ЃЈ3ЃЉЧыаДГіЫљгавдABЮЊБпЧвгыЁїABCШЋЕШЕФШ§НЧаЮЕФЕкШ§ИіЖЅЕуЃЈВЛгыCжиКЯЃЉЕФзјБъЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж8ЗжЃЉ
дквЛДЮдЫЪфШЮЮёжаЃЌвЛСОЦћГЕНЋвЛХњЛѕЮяДгМзЕидЫЭљввЕиЃЌЕНДяввЕиаЖЛѕКѓЗЕЛиЃЎЩшЦћГЕДгМзЕиГіЗЂ![]() ЃЈhЃЉЪБЃЌЦћГЕгыМзЕиЕФОрРыЮЊ
ЃЈhЃЉЪБЃЌЦћГЕгыМзЕиЕФОрРыЮЊ![]() ЃЈkmЃЉЃЌ
ЃЈkmЃЉЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
ЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
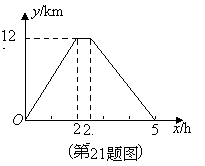
ИљОнЭМЯѓаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетСОЦћГЕЕФЭљЁЂЗЕЫйЖШЪЧЗёЯрЭЌЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧѓЗЕГЬжа![]() гы
гы![]() жЎМфЕФКЏЪ§БэДяЪНЃЛ
жЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉЧѓетСОЦћГЕДгМзЕиГіЗЂ4hЪБгыМзЕиЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗНИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФе§ЗНаЮЃЌУПИіаЁе§ЗНаЮЕФЖЅЕуНаИёЕуЃЌЁїABCЕФЖЅЕуОљдкИёЕуЩЯЃЎ 
ЃЈ1ЃЉЛГіНЋЁїABCЯђгвЦНвЦ2ИіЕЅЮЛКѓЕУЕНЕФЁїA1B1C1 ЃЌ дйЛГіНЋЁїA1B1C1ШЦЕуB1АДФцЪБеыЗНЯђа§зЊ90ЁуКѓЫљЕУЕНЕФЁїA2B1C2ЃЛ
ЃЈ2ЃЉЧѓЯпЖЮB1C1а§зЊЕНB1C2ЕФЙ§ГЬжаЃЌЕуC1ЫљОЙ§ЕФТЗОЖГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкЖўДЮКЏЪ§y=Љ2x2+1ЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
A.ЭМЯѓПЊПкЯђЯТ
B.ЭМЯѓЕФЖдГЦжсЮЊx= ![]()
C.КЏЪ§зюДѓжЕЮЊ1
D.ЕБxЃО1ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИіЬхЛЇЙКНјвЛХњЪБСюЫЎЙћЃЌ20ЬьЯњЪлЭъБЯЃЌЫћНЋБОДЮЯњЪлЧщПіНјааСЫИњзйМЧТМЃЌИљОнЫљМЧТМЕФЪ§ОнЛцжЦШчЯТЕФКЏЪ§ЭМЯѓЃЌЦфжаШеЯњЪлСПy(ЧЇПЫ)гыЯњЪлЪБМфx(Ьь)жЎМфЕФКЏЪ§ЙиЯЕШчЭМ(1)ЫљЪОЃЌЯњЪлЕЅМлp(дЊ/ЧЇПЫ)гыЯњЪлЪБМфx(Ьь)жЎМфЕФКЏЪ§ЙиЯЕШчЭМ(2)ЫљЪОЁЃ(ЯњЪлЖю=ЯњЪлЕЅМлЁСЯњЪлСП)
(1)жБНгаДГіyгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
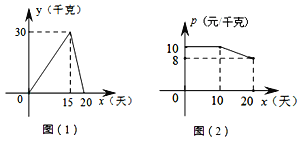
(2)ЗжБ№ЧѓЕк10ЬьКЭЕк15ЬьЕФЯњЪлЖюЃЛ
(3)ШєШеЯњЪлСПВЛЕЭгк24ЧЇПЫЕФЪБМфЖЮЮЊЁАзюМбЯњЪлЦкЁБЃЌдђДЫДЮЯњЪлЙ§ГЬжаЃЌЁАзюМбЯњЪлЦкЁБЙВгаЖрЩйЬь?дкДЫЦкМфЯњЪлЕЅМлзюИпЮЊЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЯњЪлМзЁЂввСНжжЩЬЦЗЃЌЯжгаШчЯТаХЯЂЃК ЧыНсКЯвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓМзЁЂввСНжжЩЬЦЗЕФНјЛѕЕЅМлЃЛ
ЃЈ2ЃЉвбжЊМзЁЂввСНжжЩЬЦЗЕФСуЪлЕЅМлЗжБ№ЮЊ2дЊЁЂ3дЊЃЌИУЩЬЕъЦНОљУПЬьТєГіМзЩЬЦЗ500МўКЭввЩЬЦЗ1300МўЃЌОЪаГЁЕїВщЗЂЯжЃЌМзжжЩЬЦЗСуЪлЕЅМлУПНЕ0.1дЊЃЌМзжжЩЬЦЗУПЬьПЩЖрЯњЪл100МўЃЌЩЬЕъОіЖЈАбМзжжЩЬЦЗЕФСуЪлЕЅМлЯТНЕmЃЈmЃО0ЃЉдЊЃЌдкВЛПМТЧЦфЫћвђЫиЕФЬѕМўЯТЃЌЧѓЕБmЮЊКЮжЕЪБЃЌЩЬЕъУПЬьЯњЪлМзЁЂввСНжжЩЬЦЗЛёШЁЕФзмРћШѓЮЊ1800дЊЃЈзЂЃКЕЅМўРћШѓ=СуЪлЕЅМлЉНјЛѕЕЅМлЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+2x+2kЉ2=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЃЈ1ЃЉЧѓkЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШєkЮЊе§ећЪ§ЃЌЧѓИУЗНГЬЕФИљЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com