
ЎҫМвДҝЎҝДіёцМ廧№әҪшТ»ЕъКұБоЛ®№ыЈ¬20МмПъКЫНкұПЈ¬ЛыҪ«ұҫҙОПъКЫЗйҝцҪшРРБЛёъЧЩјЗВјЈ¬ёщҫЭЛщјЗВјөДКэҫЭ»жЦЖИзПВөДәҜКэНјПуЈ¬ЖдЦРИХПъКЫБҝy(З§ҝЛ)УлПъКЫКұјдx(Мм)Ц®јдөДәҜКэ№ШПөИзНј(1)ЛщКҫЈ¬ПъКЫөҘјЫp(ФӘ/З§ҝЛ)УлПъКЫКұјдx(Мм)Ц®јдөДәҜКэ№ШПөИзНј(2)ЛщКҫЎЈ(ПъКЫ¶о=ПъКЫөҘјЫЎБПъКЫБҝ)
(1)ЦұҪУРҙіцyУлxЦ®јдөДәҜКэҪвОцКҪЈ»
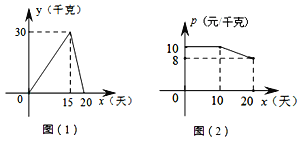
(2)·ЦұрЗуөЪ10МмәНөЪ15МмөДПъКЫ¶оЈ»
(3)ИфИХПъКЫБҝІ»өНУЪ24З§ҝЛөДКұјд¶ООӘЎ°ЧојСПъКЫЖЪЎұЈ¬ФтҙЛҙОПъКЫ№эіМЦРЈ¬Ў°ЧојСПъКЫЖЪЎұ№ІУР¶аЙЩМм?ФЪҙЛЖЪјдПъКЫөҘјЫЧоёЯОӘ¶аЙЩФӘ?
Ўҫҙр°ёЎҝҪвЈәЈЁ1Ј©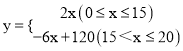 ЎЈ
ЎЈ
ЈЁ2Ј©ЎЯөЪ10МмәНөЪ15МмФЪөЪ10МмәНөЪ20МмЦ®јдЈ¬
Ўаөұ10ЎЬxЎЬ20КұЈ¬ЙиПъКЫөҘјЫpЈЁФӘ/З§ҝЛЈ©УлПъКЫКұјдxЈЁМмЈ©Ц®јдөДәҜКэҪвОцКҪОӘp=mx+nЈ¬
ЎЯөгЈЁ10Ј¬10Ј©Ј¬ЈЁ20Ј¬8Ј©ФЪz=mx+nөДНјПуЙПЈ¬
Ўа![]() Ј¬ҪвөГЈә
Ј¬ҪвөГЈә 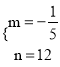 ЎЈ
ЎЈ
Ўа![]() ЎЈ
ЎЈ
өұx=10КұЈ¬ ![]() Ј¬y=2ЎБ10=20Ј¬ПъКЫҪр¶оОӘЈә10ЎБ20=200ЈЁФӘЈ©Ј»
Ј¬y=2ЎБ10=20Ј¬ПъКЫҪр¶оОӘЈә10ЎБ20=200ЈЁФӘЈ©Ј»
өұx=15КұЈ¬ ![]() Ј¬y=2ЎБ15=30Ј¬ПъКЫҪр¶оОӘЈә9ЎБ30=270ЈЁФӘЈ©ЎЈ
Ј¬y=2ЎБ15=30Ј¬ПъКЫҪр¶оОӘЈә9ЎБ30=270ЈЁФӘЈ©ЎЈ
№КөЪ10МмәНөЪ15МмөДПъКЫҪр¶о·ЦұрОӘ200ФӘЈ¬270ФӘЎЈ
ЈЁ3Ј©ИфИХПъКЫБҝІ»өНУЪ24З§ҝЛЈ¬ФтyЎЭ24ЎЈ
өұ0ЎЬxЎЬ15КұЈ¬y=2xЈ¬
ҪвІ»өИКҪ2xЎЭ24Ј¬өГxЎЭ12Ј»
өұ15ЈјxЎЬ20КұЈ¬y=©Ғ6x+120Ј¬
ҪвІ»өИКҪ©Ғ6x+120ЎЭ24Ј¬өГxЎЬ16ЎЈ
Ўа12ЎЬxЎЬ16ЎЈ
ЎаЎ°ЧојСПъКЫЖЪЎұ№ІУРЈә16©Ғ12+1=5ЈЁМмЈ©ЎЈ
ЎЯ![]() ЈЁ10ЎЬxЎЬ20Ј©ЦР
ЈЁ10ЎЬxЎЬ20Ј©ЦР![]() Јј0Ј¬ЎаpЛжxөДФцҙу¶шјхРЎЎЈ
Јј0Ј¬ЎаpЛжxөДФцҙу¶шјхРЎЎЈ
Ўаөұ12ЎЬxЎЬ16КұЈ¬xИЎ12КұЈ¬pУРЧоҙуЦөЈ¬ҙЛКұ![]() =9.6ЈЁФӘ/З§ҝЛЈ©ЎЈ
=9.6ЈЁФӘ/З§ҝЛЈ©ЎЈ
№КҙЛҙОПъКЫ№эіМЦРЎ°ЧојСПъКЫЖЪЎұ№ІУР5МмЈ¬ФЪҙЛЖЪјдПъКЫөҘјЫЧоёЯОӘ9.6ФӘ
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©·ЦБҪЦЦЗйҝцҪшРРМЦВЫЈәўЩ0ЎЬxЎЬ15Ј»ўЪ15ЈјxЎЬ20Ј¬Хл¶ФГҝТ»ЦЦЗйҝцЈ¬¶јҝЙТФПИЙиіцәҜКэөДҪвОцКҪЈ¬ФЩҪ«ТСЦӘөгөДЧшұкҙъИлЈ¬АыУГҙэ¶ЁПөКэ·ЁЗуҪвЈә
ўЩөұ0ЎЬxЎЬ15КұЈ¬ЙиИХПъКЫБҝyУлПъКЫКұјдxөДәҜКэҪвОцКҪОӘy=k1xЈ¬
ЎЯЦұПЯy=k1x№эөгЈЁ15Ј¬30Ј©Ј¬Ўа15k1=30Ј¬ҪвөГk1=2ЎЈ
Ўаy=2xЈЁ0ЎЬxЎЬ15Ј©Ј»
ўЪөұ15ЈјxЎЬ20КұЈ¬ЙиИХПъКЫБҝyУлПъКЫКұјдxөДәҜКэҪвОцКҪОӘy=k2x+bЈ¬
ЎЯөгЈЁ15Ј¬30Ј©Ј¬ЈЁ20Ј¬0Ј©ФЪy=k2x+bөДНјПуЙПЈ¬
Ўа![]() Ј¬ҪвөГЈә
Ј¬ҪвөГЈә ![]() ЎЈ
ЎЈ
Ўаy=©Ғ6x+120ЈЁ15ЈјxЎЬ20Ј©ЎЈ
ЧЫЙПЛщКцЈ¬ҝЙЦӘyУлxЦ®јдөДәҜКэ№ШПөКҪОӘЈә 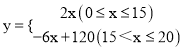 ЎЈ
ЎЈ
ЈЁ2Ј©ИХПъКЫҪр¶о=ИХПъКЫөҘјЫЎБИХПъКЫБҝЈ®УЙУЪөЪ10МмәНөЪ15МмФЪөЪ10МмәНөЪ20МмЦ®јдЈ¬өұ10ЎЬxЎЬ20КұЈ¬ЙиПъКЫөҘјЫpЈЁФӘ/З§ҝЛЈ©УлПъКЫКұјдxЈЁМмЈ©Ц®јдөДәҜКэ№ШПөКҪОӘp=mx+nЈ¬УЙөгЈЁ10Ј¬10Ј©Ј¬ЈЁ20Ј¬8Ј©ФЪp=mx+nөДНјПуЙПЈ¬АыУГҙэ¶ЁПөКэ·ЁЗуөГpУлxөДәҜКэҪвОцКҪЈ¬јМ¶шЗуөГ10МмУлөЪ15МмөДПъКЫҪр¶оЎЈ
ЈЁ3Ј©ИХПъКЫБҝІ»өНУЪ24З§ҝЛЈ¬јҙyЎЭ24Ј®ПИҪвІ»өИКҪ2xЎЭ24Ј¬өГxЎЭ12Ј¬ФЩҪвІ»өИКҪ©Ғ6x+120ЎЭ24Ј¬өГxЎЬ16Ј¬ФтЗуіцЎ°ЧојСПъКЫЖЪЎұ№ІУР5МмЈ»И»әуёщҫЭ![]() ЈЁ10ЎЬxЎЬ20Ј©Ј¬АыУГТ»ҙОәҜКэөДРФЦКЈ¬јҙҝЙЗуіцФЪҙЛЖЪјдПъКЫКұөҘјЫөДЧоёЯЦөЎЈ
ЈЁ10ЎЬxЎЬ20Ј©Ј¬АыУГТ»ҙОәҜКэөДРФЦКЈ¬јҙҝЙЗуіцФЪҙЛЖЪјдПъКЫКұөҘјЫөДЧоёЯЦөЎЈ


 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЧЎўТТБҪ№ӨіМ¶УО¬РЮН¬Т»¶ОВ·ГжЈ¬јЧ¶УПИЗеАнВ·ГжЈ¬ТТ¶УФЪјЧ¶УЗеАнәуЖМЙиВ·ГжЈ®ТТ¶УФЪЦРНҫНЈ№ӨБЛТ»¶ОКұјдЈ¬И»әу°ҙНЈ№ӨЗ°өД№ӨЧчР§ВКјМРш№ӨЧчЈ®ФЪХыёц№ӨЧч№эіМЦРЈ¬јЧ¶УЗеАнНкөДВ·ГжіӨyЈЁГЧЈ©УлКұјдxЈЁКұЈ©өДәҜКэНјПуОӘПЯ¶ОOAЈ¬ТТ¶УЖМЙиНкөДВ·ГжіӨyЈЁГЧЈ©УлКұјдxЈЁКұЈ©өДәҜКэНјПуОӘХЫПЯBC-CD-DEЈ¬ИзНјЛщКҫЈ¬ҙУјЧ¶УҝӘКј№ӨЧчКұјЖКұЈ®
ЈЁ1Ј©·ЦұрЗуПЯ¶ОBCЎўDEЛщФЪЦұПЯ¶ФУҰөДәҜКэ№ШПөКҪЈ®
ЈЁ2Ј©өұјЧ¶УЗеАнНкВ·ГжКұЈ¬ЗуТТ¶УЖМЙиНкөДВ·ГжіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝёщҫЭПВБРТӘЗуЈ¬ҪвҙрПа№ШОКМвЈ®
ЗлІ№И«ТФПВЗуІ»өИКҪ©Ғ2x2©Ғ4xЈҫ0өДҪвјҜөД№эіМЈ®
ўЩ№№ФмәҜКэЈ¬»ӯіцНјПуЈәёщҫЭІ»өИКҪМШХч№№Фм¶юҙОәҜКэy=©Ғ2x2©Ғ4xЈ»ІўФЪПВГжөДЧшұкПөЦРЈЁНј1Ј©»ӯіц¶юҙОәҜКэy=©Ғ2x2©Ғ4xөДНјПуЈЁЦ»»ӯіцНјПујҙҝЙЈ©Ј®
ўЪЗуөГҪзөгЈ¬ұкКҫЛщРиЈ¬өұy=0КұЈ¬ЗуөГ·ҪіМ©Ғ2x2©Ғ4x=0өДҪвОӘЈ»ІўУГҫвіЭПЯұкКҫіцәҜКэy=©Ғ2x2©Ғ4xНјПуЦРyЈҫ0өДІҝ·ЦЈ®
ўЫҪиЦъНјПуЈ¬РҙіцҪвјҜЈәУЙЛщұкКҫНјПуЈ¬ҝЙөГІ»өИКҪ©Ғ2x2©Ғ4xЈҫ0өДҪвјҜОӘ©Ғ2ЈјxЈј0Ј®ЗлДгАыУГЙПГжЗуТ»ФӘТ»ҙОІ»өИКҪҪвјҜөД№эіМЈ¬ЗуІ»өИКҪx2©Ғ2x+1ЎЭ4өДҪвјҜЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶Ф·ЗёәКөКэxЎ°ЛДЙбОеИлЎұөҪёцО»өДЦөјЗОӘЈјxЈҫЈ¬јҙЈәөұnОӘ·ЗёәХыКэКұЈ¬Из№ыn©Ғ ![]() ЎЬxЈјn+
ЎЬxЈјn+ ![]() Ј¬ФтЈјxЈҫ=nЈ® ИзЈәЈј0Јҫ=Јј0.48Јҫ=0Ј¬Јј0.64Јҫ=Јј1.493Јҫ=1Ј¬Јј2Јҫ=2Ј¬Јј3.5Јҫ=Јј4.12Јҫ=4Ј¬Ўӯ
Ј¬ФтЈјxЈҫ=nЈ® ИзЈәЈј0Јҫ=Јј0.48Јҫ=0Ј¬Јј0.64Јҫ=Јј1.493Јҫ=1Ј¬Јј2Јҫ=2Ј¬Јј3.5Јҫ=Јј4.12Јҫ=4Ј¬Ўӯ
КФҪвҫцПВБРОКМвЈә
ЈЁ1Ј©МоҝХЈәўЩЈјҰРЈҫ=________Ј»ўЪИз№ыЈј2x©Ғ1Јҫ=3Ј¬ФтКөКэxөДИЎЦө·¶О§ОӘ________Ј»
ЈЁ2Ј©ўЩөұxЎЭ0Ј¬mОӘ·ЗёәХыКэКұЈ¬ЗуЦӨЈәЈјx+mЈҫ=m+ЈјxЈҫЈ»ўЪҫЩАэЛөГчЈјx+yЈҫ=ЈјxЈҫ+ЈјyЈҫІ»әгіЙБўЈ»
ЈЁ3Ј©ЗуВъЧгЈјxЈҫ= ![]() xөДЛщУР·ЗёәКөКэxөДЦөЈ®
xөДЛщУР·ЗёәКөКэxөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎПACB=60ЎгЈ¬°лҫ¶ОӘ1cmөДЎСOЗРBCУЪөгCЈ¬ИфҪ«ЎСOФЪCBЙППтУТ№ц¶ҜЈ¬Фтөұ№ц¶ҜөҪЎСOУлCAТІПаЗРКұЈ¬ФІРДOТЖ¶ҜөДЛ®ЖҪҫаАлКЗcmЈ® 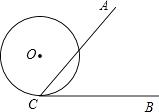
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЎчABCЦРЈ¬ЎПBAC=78ЎгЈ¬AB=ACЈ¬PОӘЎчABCДЪТ»өгЈ¬Б¬BPЈ¬CPЈ¬К№ЎПPBC=9ЎгЈ¬ЎПPCB=30ЎгЈ¬Б¬PAЈ¬ФтЎПBAPөД¶ИКэОӘ_______Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶юҙОәҜКэy=ax2+bx+cЈЁaЎЩ0Ј©өДНјПуИзНјЛщКҫЈ¬ёщҫЭНјПу»ШҙрПВБРОКМвЈ® 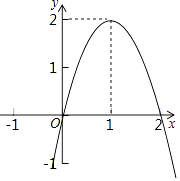
ЈЁ1Ј©Рҙіц·ҪіМax2+bx+c=0өДёщЈ»
ЈЁ2Ј©РҙіцІ»өИКҪax2+bx+cЈј0өДҪвјҜЈ»
ЈЁ3Ј©Иф·ҪіМax2+bx+c=kОЮКөКэёщЈ¬РҙіцkөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ұЯіӨОӘ1өДХэОеұЯРОABCDEЈ¬¶ҘөгAЎўBФЪ°лҫ¶ОӘ1өДФІЙПЈ¬ЖдЛьёчөгФЪФІДЪЈ¬Ҫ«ХэОеұЯРОABCDEИЖөгAДжКұХлРэЧӘЈ¬өұөгEөЪТ»ҙОВдФЪФІЙПКұЈ¬ФтөгCЧӘ№эөД¶ИКэОӘ Ј® 
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎчABEәНЎчADCКЗЎчABC·ЦұрСШЧЕABЎўACұЯ·ӯХЫ180ЎгРОіЙөДЈ¬ИфЎП1ЈәЎП2ЈәЎП3=28Јә5Јә3Ј¬ФтЎПҰБөД¶ИКэОӘ__¶ИЈ®

Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com