
【题目】如图△ABC中,∠BAC=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为_______.

【答案】69°
【解析】
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC,根据等边三角形的性质得到AD=AB=AC,求出∠DAC、∠ACD、∠ADC的度数,根据三角形的内角和定理求出∠ABC=∠ACB=51°,即∠CDB=141°=∠BPC,再证△BDC≌△BPC,得到PC=DC,进一步得到等边△DPC,推出△APD≌△APC,根据全等三角形的性质得到∠DAP=∠CAP=9°,即可求出答案.
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC
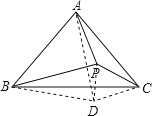
∴AD=AB=AC,![]()
![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴△BDC≌△BPC,
∴PC=DC,
又∵![]()
∴△DPC是等边三角形,
∴△APD≌△APC,
∴![]()
∴![]()
故答案为:69°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的边长为12,点P为AC上一点,点D在CB的延长线上,且BD=AP,连接PD交AB于点E,PE⊥AB于点F,则线段EF的长为( )

A. 6 B. 5
C. 4.5 D. 与AP的长度有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发![]() (h)时,汽车与甲地的距离为
(h)时,汽车与甲地的距离为![]() (km),
(km),![]() 与
与![]() 的函数关系如图所示.
的函数关系如图所示.
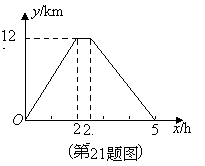
根据图象信息,解答下列问题:
(1)这辆汽车的往、返速度是否相同?请说明理由;
(2)求返程中![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)求这辆汽车从甲地出发4h时与甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=﹣2x2+1,下列说法错误的是( )
A.图象开口向下
B.图象的对称轴为x= ![]()
C.函数最大值为1
D.当x>1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体户购进一批时令水果,20天销售完毕,他将本次销售情况进行了跟踪记录,根据所记录的数据绘制如下的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图(1)所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图(2)所示。(销售额=销售单价×销售量)
(1)直接写出y与x之间的函数解析式;
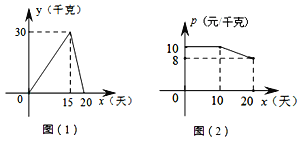
(2)分别求第10天和第15天的销售额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中,“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)

(1)若点C与点A关于原点O对称,则点C的坐标为 ;
(2)将点A向右平移5个单位得到点D,则点D的坐标为 ;
(3)由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售甲、乙两种商品,现有如下信息: 请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一段圆弧形弯道,弯道长12π米,圆弧所对的圆心角是81°. 
(1)用直尺和圆规作出圆弧所在的圆心O;(不写作法,保留作图痕迹)
(2)求这段圆弧的半径R.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,顶点为M. 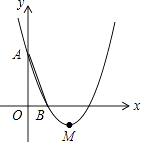
(1)则b= , c=;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com