练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图为一段圆弧形弯道，弯道长12π米，圆弧所对的圆心角是81°．
    （1）用直尺和圆规作出圆弧所在的圆心O；（不写作法，保留作图痕迹）
    （2）求这段圆弧的半径R．

    【答案】
    （1）解：如图，点O即为所求点；


    （2）解：根据题意得： =12π，

    解得：R= ，

    答：这段圆弧的半径为 米


    【解析】（1）弧上任取三点A、B、C，连结AB、BC，分别作AB和BC的垂直平分线，两垂直平分线的交点为点O；（2）根据弧长公式列出关于R的方程，解之可得．
    【考点精析】解答此题的关键在于理解垂径定理的相关知识，掌握垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧，以及对圆心角、弧、弦的关系的理解，了解在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，同弧等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，对称轴为直线x=﹣1，与x轴的一个交点为（1，0），与y轴的交点为（0，3），则方程ax2+bx+c=0（a≠0）的解为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图△ABC中，∠BAC=78°，AB=AC，P为△ABC内一点，连BP，CP，使∠PBC=9°，∠PCB=30°，连PA，则∠BAP的度数为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在6×8的网格图中，每个小正方形边长均为1，原点O和△ABC的顶点均为格点．

    （1）以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′与△ABC位似，且位似比为1：2；（保留作图痕迹，不要求写作法和证明）
    （2）若点C和坐标为（2，4），则点A′的坐标为（ ， ），点C′的坐标为（ ， ），S△A′B′C′：S△ABC= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为1的正五边形ABCDE，顶点A、B在半径为1的圆上，其它各点在圆内，将正五边形ABCDE绕点A逆时针旋转，当点E第一次落在圆上时，则点C转过的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x= ，且经过点（2，0），下列说法： ①abc＜0；
    ②a+b=0；
    ③4a+2b+c＜0；
    ④若（﹣2，y1），（﹣3，y2）是抛物线上的两点，则y1＜y2 ，
    其中说法正确的是（ ）

    A.①②④
    B.③④
    C.①③④
    D.①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费(元)与用水量(吨)的函数关系如图所示。

    (1)分别写出当和时，与的函数关系式；

    (2)若某用户该月用水21吨，则应交水费多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC 中，AB=AC，∠BAC=90°，D 是BC 上一点，EC⊥BC，EC=BD，DF=FE．

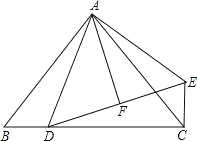
    求证：（1）△ABD≌△ACE；

    （2）AF⊥DE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB：y=﹣x﹣b分别与x，y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1．

    （1）求点B的坐标；
    （2）求直线BC的解析式；
    （3）直线EF：y=2x﹣k（k≠0）交AB于E，交BC于点F，交x轴于点D，是否存在这样的直线EF，使得S△EBD=S△FBD？若存在，求出k的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案