
【题目】如图,在平面直角坐标系中,已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,顶点为M. 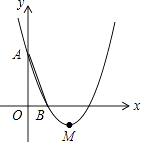
(1)则b= , c=;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式.
【答案】
(1)4;3
(2)解:∵A(0,3),B(1,0),
∴OA=3,OB=1.
∴旋转后C点的坐标为(4,1).
当x=4时,y=x2﹣4x+3=42﹣4×4+3=3,
∴抛物线y=x2﹣4x+3经过点(4,3).
∴将原抛物线沿y轴向下平移2个单位后过点C.
∴平移后的抛物线解析式为y=x2﹣4x+1
【解析】解:(1)已知抛物线y=x2﹣bx+c经过A(0,3),B(1,0)两点,∴ ![]() 解得:
解得: ![]() ,∴b、c的值分别为4,3.故答案是:4;3.
,∴b、c的值分别为4,3.故答案是:4;3.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠BAC=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交交费![]() (元)与用水量
(元)与用水量![]() (吨)的函数关系如图所示。
(吨)的函数关系如图所示。
(1)分别写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
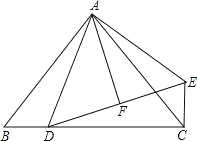
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=![]() x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________
x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=﹣x﹣b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x﹣k(k≠0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为km . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com