
【题目】如图,等腰直角△ABC中,∠ACB=90°,点D在BA的延长线上,连接CD,过点C作CE⊥CD,使CE=CD,连接BE,若点N为BD的中点,连接CN、BE.
(1)求证:AB⊥BE.
(2)求证:AE=2CN.

【答案】见解析
【解析】
(1)证明△DCA与△ECB全等,再利用全等三角形的性质证明即可;
(2)延长CN至点K,使NK=CN,连接DK,利用已知条件证明△DNK≌△BNC,所以可得DK=BC=AC,∠KDC+∠DCB=180°,又因为∠DCK=∠ACE,DK=AC,CD=CE,由三角形的全等可得AE=CK,所以AE=2CN.
证明:(1)∵CE⊥CD,∠ACB=90°,
∴∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠BCE+∠ACE,
∴∠DCA=∠BCE,
在△DCA与△ECB中,
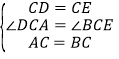 ,
,
∴△DCA≌△ECB(SAS),
∴∠CDA=∠CEB,∠DAC=∠EBC=135°,
∴∠ABE=∠CBE-∠ABC=135°-45°=90°,
∴AB⊥BE;
(2)延长CN至点K,使NK=CN,连接DK.
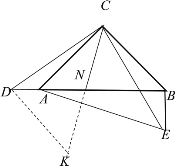
∵∠DCA+∠ACE=90°,∠BCE+∠ACE=90°,
∴∠DCB+∠ACE=180°,
∴∠KDN=∠CBN,
∴DK∥BC,
∵在△DNK与△BNC中,
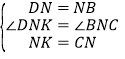
∴△DNK≌△BNC,
∴DK=BC=AC,
∴∠KDC+∠DCB=180°,
∵∠DCK=∠ACE,
又∵DK=AC,CD=CE,
∵△KDC≌△ACE,
∴AE=CK,
∴AE=2CN.


科目:初中数学 来源: 题型:
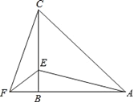
【题目】在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:△ABE≌△CBF;
(2)若∠CAE=25°,求∠BFC度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A=90°,BC∥AD,AB=6cm,点P从A出发沿射线AD运动,速度是每秒1cm,点R从点B出发沿射线BC运动,速度是每秒2cm,点Q在点P的右侧,且PQ=10cm,时间为t秒;
求:(1)△PQR的面积;
(2)当t=1秒时,求PR的长;
(3)当t为何值时,△PQR是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P , 若EF=2,则梯形ABCD的周长为( ) 
A.12
B.10
C.8
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )
A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,真命题是( ) 
A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点P(﹣5,3)向右平移8个单位得到点P1 , 再将点P1绕原点旋转90°得到点P2 , 则点P2的坐标是( )
A.(3,﹣3)
B.(﹣3,3)
C.(3,3)或(﹣3,﹣3)
D.(3,﹣3)或(﹣3,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com