
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.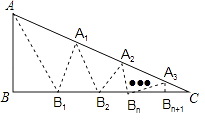
(1)若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(2)若一个三角形的最小角是4°,且该三角形的三个角均是此三角形的好角.请写出符合要求三角形的另两个角的度数 . (写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.
a.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是矩形.
b.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是菱形.
c.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图象经过(-4,-9)和(3,5)两点.
①求一次函数解析式.
②求图象和坐标轴交点坐标.并画出图象.
③求图象和坐标轴围成三角形面积.
④若点(2,a)在函数图象上,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
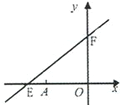
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好放松心情,上周六,小红妈妈开车带着小红一家到外郊游,出发前汽车油箱内有一定量的油.行驶过程中油箱中剩余油量![]() (升)与行驶时间
(升)与行驶时间![]() (小时)的关系如下表,请根据表格回答下列问题:
(小时)的关系如下表,请根据表格回答下列问题:
时间/小时 | 0 | 1 | 2 | 3 | 4 | 5 |
邮箱剩余油量/升 | 50 | 45 | 40 | 35 | 30 | 25 |
(1)汽车行驶前油箱里有_____________升汽油,汽车每小时耗油____________升;
(2)请写出![]() 与
与![]() 的关系式;
的关系式;
(3)当汽车行驶24小时时,油箱中还剩余多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
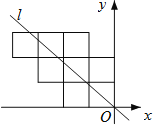
A.y=﹣x B.y=﹣![]() x C.y=﹣
x C.y=﹣![]() x D.y=﹣
x D.y=﹣![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com