
【题目】已知一次函数图象经过(-4,-9)和(3,5)两点.
①求一次函数解析式.
②求图象和坐标轴交点坐标.并画出图象.
③求图象和坐标轴围成三角形面积.
④若点(2,a)在函数图象上,求a的值.
【答案】(1)y=2x-1;(2)A(0,-1),B(0.5,0);(3)面积为0.25;(4)a=3.
【解析】
(1)根据待定系数法求解即可;
(2)分别令x、y等于0,求出y与x的值,即可得到图象与y轴和x轴的交点;
(3)求出三角形在坐标轴上的边的长度,再代入三角形面积公式计算即可;
(4)把点(a,2)的坐标代入函数解析式求解即可.
(1)设一次函数解析式为y=kx+b,把点(3,5),(﹣4,﹣9)分别代入解析式得:则![]() ,解得:
,解得:![]() ,∴一次函数解析式为y=2x﹣1;
,∴一次函数解析式为y=2x﹣1;
(2)当x=0时,y=﹣1,当y=0时,2x﹣1=0,解得:x![]() 0.5,∴与坐标轴的交点为A(0,﹣1)、B(0.5,0);图象如图:
0.5,∴与坐标轴的交点为A(0,﹣1)、B(0.5,0);图象如图:
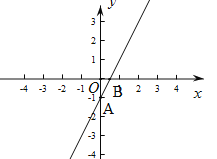
(3)S△![]() |﹣1|
|﹣1|![]() 0.25;
0.25;
(4)∵点(2,a)在图象上,∴a=2×2﹣1=3,∴a![]() 3.
3.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).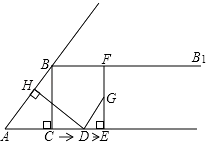
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t> ![]() 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
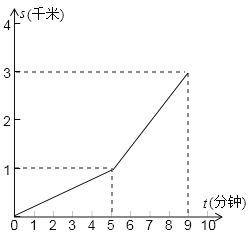
【题目】小明从家骑车上学,先匀速上坡到达![]() 地后再匀速下坡到达学校,所用的时间与路程如图所示,如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是( )
地后再匀速下坡到达学校,所用的时间与路程如图所示,如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是( )
A.9分钟B.12分钟C.8分钟D.10分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
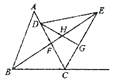
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() ,
,![]() 平分
平分![]() 的外角,且
的外角,且![]() .连接
.连接![]() 交
交![]() 于
于![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,则
,则![]() 平分
平分![]() 正确的是_____________.
正确的是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
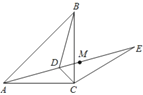
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15o,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM。则下列结论:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分AB;④ME=BD;正确的有( )
A. 1个B. 4个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
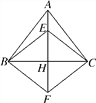
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com