
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C����������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F������DF�����˶���ʱ��Ϊt�루t��0����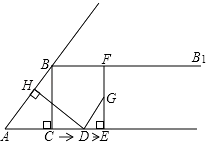
��1����tΪʱ��AD=AB����ʱDE�ij���Ϊ��
��2������DEF���ACBȫ��ʱ����t��ֵ��
��3����DH����ֱ��Ϊ�Գ��ᣬ�߶�AC����ԳƱ任���ͼ��ΪA��C�䣮
�ٵ�t�� ![]() ʱ�����ADA������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
ʱ�����ADA������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
�۵��߶�A��C��������BB1�й�����ʱ����t��ȡֵ��Χ��
���𰸡�
��1��2,2
��2���⣺�ߡ�ACB=90�㣬BB1��AC��EF��AC��
���ı���BCEF�Ǿ��Σ�EF=BC=8��
��AD��AEʱ��5t��6+3t��
��0��t��3��
��DE=AC����ACB�ա�DEF��DE=AE��AD=6+3t��5t=6��2t��
��6��2t=6��
��t=0��
��t��0���������⣬�ᣩ��
��AD��AEʱ��5t��6+3t��
��t��3��
��DE=AC����ACB�ա�DEF��DE=AD��AE=5t��6��3t=2t��6��
��2t��6=6��
��t=6��
�൱t=6ʱ����DEF���ACBȫ�ȣ�
��3���⣺����ͼ��
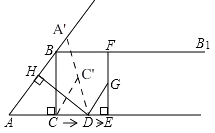
�ߡ�ACB=��AHD����BAC=��DAH��
���ABC�ס�ADH��
�� ![]() ��
��
�� ![]() ��
��
��AH=3t��DH=4t��
��S��ADA'=2S��ADH=2�� ![]() AH��DH=AH��DH=12t2��
AH��DH=AH��DH=12t2��
�ڵ���A'��������BB1�ϵĵ�Bʱ��AA'=AB=10��
��DH��AB��
��AA'=2AH=2��5t��cos��A=6t=10��
��t= ![]() ��
��
����C'��������BB1��ʱ��CC'��AB��
��BB1��AC��
���ı���ACC'BΪƽ���ı��Σ�
��CC'=AB=10��
��CC'=2CD��cos��A=2����5t��6���� ![]() =
= ![]() ��5t��6����
��5t��6����
��t= ![]() ��
��
�� ![]() ��t��
��t�� ![]() ���߶�A'C'������BB1�й����㣮
���߶�A'C'������BB1�й����㣮
���������⣺��1����Rt��ABC�У�AC=6��BC=8�����ݹ��ɶ����ã�AB= ![]() =10��
=10��
���˶�֪��AD=5t��
��AD=AB��
��5t=10��
��t=2��
��CD=AD��AC=10��6=4��CE=3t=6��
��DE=CE��CD=2��
���Դ���2��2��
�����㾫�����������⣬������Ҫ�˽�ƽ���ı��ε��ж�(����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı���)����Ҫ������ԳƵ�����(����ij��ֱ�߶ԳƵ�����ͼ����ȫ���Σ��������ͼ�ι���ijֱ�߶Գƣ���ô�Գ����Ƕ�Ӧ�����ߵĴ�ֱƽ���ߣ�����ͼ�ι���ijֱ�߶Գƣ�������ǵĶ�Ӧ�߶λ��ӳ����ཻ����ô�����ڶԳ�����)�����֪ʶ���Ǵ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BAE����AED��180�㣬��1����2����ô��M����N���������������̣�������գ�
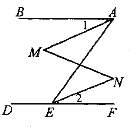
�⣺�ߡ�BAE����AED��180�� ����֪�� ��
��AB//DE( ���� ���� )��
����BAE�� ( ���� ���� )
�� �ߡ�1����2����֪��
���BAE����1�� �� ���� �� ����ʽ���ʣ���
����MAE����NEA��
�� �� �� ���� ���� ����
���M����N����ֱ��ƽ�У��ڴ�����ȣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼֱ��l1�Ľ���ʽΪy=x+1��ֱ��l2�Ľ���ʽΪy=ax+b��a��0����������ͼ����y����һ��C��ֱ��l2��x��Ľ���B��2��0��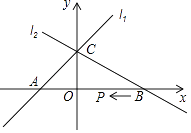
��1����a��b��ֵ��
��2��������Q��n��0���Ҵ�ֱ��x���ֱ����l1��l2�ֱ��ڵ�M��N��λ��x���Ϸ�ʱ����n��ȡֵ��Χ��
��3������P�ӵ�B������x����ÿ��1����λ�����ٶ������ƶ������ƶ�ʱ��Ϊt�룬����PACΪ����������ʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������и��⣮
��1�����ı��ʽ��ֵ�������з��Ӻͷ�ĸ����ߴε�ϵ������Ϊ����![]() ________��
________��
��2�����ı��ʽ��ֵ�������з��Ӻͷ�ĸ���и���ϵ������Ϊ����![]() ________��
________��
��3������ʽ![]() ��ֵ��������������
��ֵ��������������![]() ��ֵ��
��ֵ��
��4����֪![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У��ء�BAC��ƽ����AB1�۵��������ظ����֣������²����ء�B1A1C��ƽ����A1B2�۵��������ظ����֡������²����ء�BnAnC��ƽ����AnBn+1�۵�����Bn���C�غϣ������۵����ٴΣ�ֻҪ���һ��ǡ���غϣ���ơ�BAC�ǡ�ABC�ĺýǣ�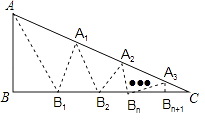
��1��������n���۵���BAC�ǡ�ABC�ĺýǣ����B���C �����B����C��֮��ĵ�����ϵΪ ��
��2����һ�������ε���С����4�㣬�Ҹ������ε������Ǿ��Ǵ������εĺýǣ���д������Ҫ�������ε��������ǵĶ��� �� ��д��һ�ּ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ���M��N�ֱ���AC��BC���е㣮
![]()
��1����AC��9cm��CB��6cm�����߶�MN�ij���
��2����CΪ�߶�AB����һ�㣬����AC+CB��acm�������������䣬���ܲ���MN�ij����𣿲�˵�����ɣ�
��3����C���߶�AB���ӳ����ϣ�������AC-BC��bcm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij������뻭��ͼ�Σ���ֱ��д����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ı���AOBC�Ǿ��Σ���OΪ����ԭ�㣬OB��OA�ֱ���x�ᡢy���ϣ���A������Ϊ��0��3������OAB=60�㣬��ABΪ����ۺ�C������D�㴦����D�������Ϊ�� ��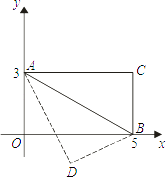
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���ͼ��(��4����9)��(3��5)���㣮
����һ�κ�������ʽ��
����ͼ��������ύ�����꣮������ͼ��
����ͼ���������Χ�������������
������(2��a)�ں���ͼ���ϣ���a��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com