
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边
边![]() 上一点,
上一点,![]() ,
,![]() 平分
平分![]() 的外角,且
的外角,且![]() .连接
.连接![]() 交
交![]() 于
于![]() 为边
为边![]() 上一点,满足
上一点,满足![]() ,连接
,连接![]() 交
交![]() 于
于![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,则
,则![]() 平分
平分![]() 正确的是_____________.
正确的是_____________.
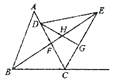
【答案】①、②、④
【解析】
①可推导∠ACB=∠ACE=60°,进而可证全等;
②先证△BFC≌△DGC,得到∠FBC=∠CDG,∠BFC=∠DFH,从而推导得出∠BCF=∠DHF=60°;
③是错误的,无法得出;
④利用△BCE的外角∠ECM和△ABC的外角∠ACM的关系,结合∠DEC=∠A可推导得出.
如下图
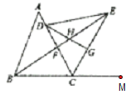
①∵∠ACB=60°,∴∠ACM=120°
∵CE是∠ACM的角平分线,∴∠ACE=∠ECM=60°
∴∠ACB=∠ACE
∵BC=DC,AC=CE
∴△ABC≌△EDC(SAS),正确;
②∵CF=CG,已知∠BCF=∠DCG=60°,BC=DC
∴△BCF≌△DCG
∴∠FBC=∠GDC
∵∠BFC=∠DFH
∴∠BCF=∠DHF=60°,正确;
③条件不足,无法得出![]() ,错误;
,错误;
④∵BE是∠DEC的角平分线,
∴∠DEF=∠CEF
∵∠ECM=∠CBF+∠FEC=60°,∠DCM=∠A+∠ABC=120°
∴∠A+∠ABC=2(∠FBC+∠FEC)=2∠FBC+2∠FEC=2∠FBC+∠DEC
∵∠DEC=∠A
∴∠ABC=2∠FBC
∴BE平分∠ABC,正确;
故答案为:①②④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】完成下列各题.
(1)不改变分式的值,把下列分子和分母的最高次的系数都化为正数![]() ________.
________.
(2)不改变分式的值,把下列分子和分母的中各项系数都化为整数![]() ________.
________.
(3)若分式![]() 的值是整数,求整数
的值是整数,求整数![]() 的值.
的值.
(4)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )

A. (42012×![]() ,42012) B. (24026×
,42012) B. (24026×![]() ,24026) C. (24026×
,24026) C. (24026×![]() ,24024) D. (44024×
,24024) D. (44024×![]() ,44024)
,44024)
查看答案和解析>>
科目:初中数学 来源: 题型:
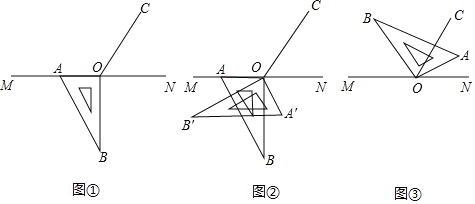
【题目】如图①,点O为直线MN上一点,过点O作直线OC,使∠NOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OA在射线OM上,另一边OB在直线AB的下方,其中∠OBA=30°
(1)将图②中的三角尺沿直线OC翻折至△A′B′O,求∠A′ON的度数;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转,旋转角为α(0<α<360°),在旋转的过程中,在第几秒时,直线OA恰好平分锐角∠NOC;
(3)将图①中的三角尺绕点O顺时针旋转,当点A点B均在直线MN上方时(如图③所示),请探究∠MOB与∠AOC之间的数量关系,请直接写出结论,不必写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图象经过(-4,-9)和(3,5)两点.
①求一次函数解析式.
②求图象和坐标轴交点坐标.并画出图象.
③求图象和坐标轴围成三角形面积.
④若点(2,a)在函数图象上,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
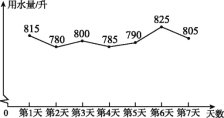

(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
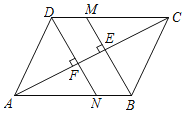
【题目】如图,在ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com