
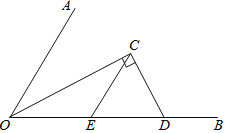
【题目】如图,![]() ,OC平分
,OC平分![]() ,C为角平分线上一点,过点C作
,C为角平分线上一点,过点C作![]() ,垂足为C,交OB于点D,
,垂足为C,交OB于点D,![]() 交OB于点E.
交OB于点E.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 若
若![]() ,求CD的长.
,求CD的长.
【答案】(1)等边三角形(2)![]()
【解析】
(1)△CED为等边三角形,理由如下:由OC为角平分线及∠AOB度数求出∠AOC与∠COE度数,再由CE与OA平行,得到一对内错角相等,再由CD与OC垂直,求出∠ECD度数,利用三个内角相等的三角形为等边三角形即可得证;
(2)由△CED为等边三角形,得到三边相等,利用等角对等边得到OE=CE,进而得到OE=CE=DE,设CD=x,利用30度角所对的直角边等于斜边的一半得到OD=2x,再由OC的长,利用勾股定理列出方程,求出方程的解得到x的值,即可确定出CD的长.
![]() 是等边三角形,理由如下:
是等边三角形,理由如下:
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形;
是等边三角形;
![]() 是等边三角形,
是等边三角形,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,根据勾股定理得:
中,根据勾股定理得:![]() ,
,
解得:![]() ,
,
则![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知动点P在函数y= ![]() (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )
(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AFBE的值为( )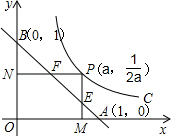
A.4
B.2
C.1
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度为 ![]() (即tan∠PCD=
(即tan∠PCD= ![]() ).
).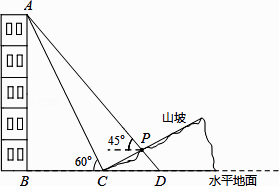
(1)求该建筑物的高度(即AB的长).
(2)求此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.
(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
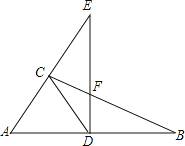
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有______
,则下列结论正确的有______ ![]() 将所有正确答案的序号都填在横线上
将所有正确答案的序号都填在横线上![]()
![]() ;
;![]() ;
;![]() 是等边三角形;
是等边三角形;![]() 若
若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
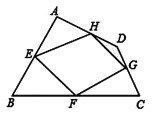
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com