
【题目】如图,AD是![]() 的角平分线,
的角平分线,![]() ,
,![]() ,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是
,垂足分别为点E、点F,连接EF与AD相交于点O,下列结论不一定成立的是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】将连续的偶数2,4,6,8……,排成如下表:

(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和,
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的“读好书,讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书.下面是七年级(1)班全体同学捐献图书的情况统计图:
请你根据以上统计图中的信息,解答下列问题:
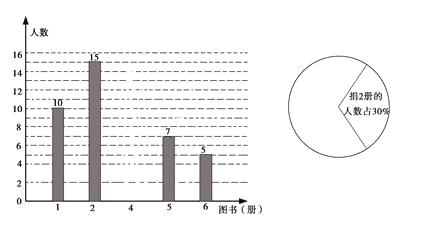
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所捐献图书的中位数和众数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
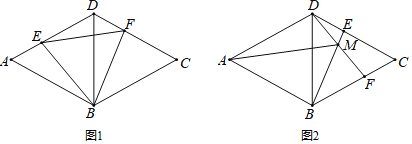
【题目】如图,已知菱形ABCD边长为4,![]() ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
![]() 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
![]() 在
在![]() 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时![]() 的面积;
的面积;
![]() 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则![]() 大小是否变化?请说明理由.
大小是否变化?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com