Question

【题目】（1）阅读理解：

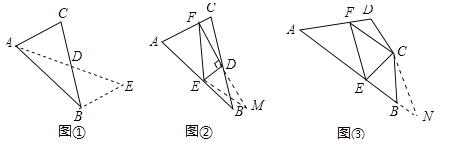
如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．

解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．

中线AD的取值范围是 ；

（2）问题解决：

如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；

（3）问题拓展：

如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以为顶点作一个70°角，角的两边分别交AB，AD于E、F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．

Answer 1

【答案】（1）2＜AD＜8；（2）证明见解析；（3）BE+DF=EF．

【解析】

试题分析：（1）延长AD至E，使DE=AD，由SAS证明△ACD≌△EBD，得出BE=AC=6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；

（2）延长FD至点M，使DM=DF，连接BM、EM，同（1）得△BMD≌△CFD，得出BM=CF，由线段垂直平分线的性质得出EM=EF，在△BME中，由三角形的三边关系得出BE+BM＞EM即可得出结论；

（3）延长AB至点N，使BN=DF，连接CN，证出∠NBC=∠D，由SAS证明△NBC≌△FDC，得出CN=CF，∠NCB=∠FCD，证出∠ECN=70°=∠ECF，再由SAS证明△NCE≌△FCE，得出EN=EF，即可得出结论．

试题解析：（1）解：延长AD至E，使DE=AD，连接BE，如图①所示：

∵AD是BC边上的中线，∴BD=CD，在△BDE和△CDA中，∵BD=CD，∠BDE=∠CDA，DE=AD，∴△BDE≌△CDA（SAS），∴BE=AC=6，在△ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，∴10﹣6＜AE＜10+6，即4＜AE＜16，∴2＜AD＜8；

故答案为：2＜AD＜8；

（2）证明：延长FD至点M，使DM=DF，连接BM、EM，如图②所示：

同（1）得：△BMD≌△CFD（SAS），∴BM=CF，∵DE⊥DF，DM=DF，∴EM=EF，在△BME中，由三角形的三边关系得：BE+BM＞EM，∴BE+CF＞EF；

（3）解：BE+DF=EF；理由如下：

延长AB至点N，使BN=DF，连接CN，如图3所示：

∵∠ABC+∠D=180°，∠NBC+∠ABC=180°，∴∠NBC=∠D，在△NBC和△FDC中，∵BN=DF，∠NBC=∠D，BC=DC，∴△NBC≌△FDC（SAS），∴CN=CF，∠NCB=∠FCD，∵∠BCD=140°，∠ECF=70°，∴∠BCE+∠FCD=70°，∴∠ECN=70°=∠ECF，在△NCE和△FCE中，∵CN=CF，∠ECN=∠ECF，CE=CE，∴△NCE≌△FCE（SAS），∴EN=EF，∵BE+BN=EN，∴BE+DF=EF．