
����Ŀ�������������
ѧϰ��������ȫ�ȵ��ж�����������SSS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о���
������˼����
���Dz����������÷������Ա�ʾΪ������ABC����DEF�У�AC=DF��BC=EF����B=��E��Ȼ����B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ�����������������̽����
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
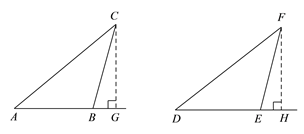
��ͼ��������ABC����DEF��AC=DF��BC=EF����B=��E=90���������� ��������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��ͼ��������ABC����DEF��AC=DF��BC=EF����B=��E������B����E���Ƕ۽ǣ�����֤������ABC�ա�DEF����ʾ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H����
���������������B�����ʱ����ABC����DEF��һ��ȫ�ȣ�
����ABC����DEF��AC=DF��BC=EF����B=��E������B����E������ǣ���������ͼ������ͼ�����ó߹�������DEF��ʹ��DEF����ABC��ȫ�ȣ�

���𰸡���1��HL����2�������������3����DEF����ABC��ȫ�ȣ�ͼ������.
�����������������
��1���������֪����ʱ�õ���Rt��ABC��Rt��DEF����������HL����
��2����ͼ���ֱ����C��CG��AB��AB���ӳ����ڵ�G������F��FH��DE��DE���ӳ�����H��Ȼ��������AAS��֤��CBG�ա�FEH����������HL��֤Rt��ACG��Rt��DFH���������AAS��֤��ABC�ա�DEF������
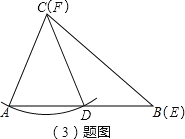
��3����ͼ3���Ե�CΪԲ�ģ�CAΪ�뾶������AB�ڵ�D�����E�͵�B�غϣ���F�͵�C�غϣ���ͼ�еġ�ABC�͡�DEF������Ŀ�е��������������ԣ���ʱ���������β���ȫ��.
���������
��1��������ABC����DEF����AC=DF��BC=EF����B=��E=90����
��Rt��ABC��Rt��DEF��HL��.
����ʱ�ж���������ȫ�ȵ���������HL��
��2����ͼ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
�ߡ�ABC=��DEF������ABC����DEF���Ƕ۽ǣ�
��180�㩁��ABC=180�㩁��DEF��
����CBG=��FEH��
����CBG����FEH�� 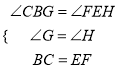 ��
��
���CBG�ա�FEH��AAS����
��CG=FH��
��Rt��ACG��Rt��DFH�� ![]() ��
��
��Rt��ACG��Rt��DFH��HL����
���A=��D��
����ABC����DEF�� 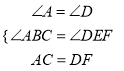 ��
��
���ABC�ա�DEF��AAS����
��3����ͼ����DEF����ABC����AC=DF��BC=EF����B=��E����������Ŀ�е��������������������Dz�ȫ��.


 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�ĶԽ��ߵĽ���������ԭ�㣬��ADƽ����x�ᣮ����A����Ϊ(-1��2)�����C������Ϊ�� ��
A. (1��-2) B. (2��-1) C. (1��-3) D. (2��-3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�������꼶ij��ѧ��ÿ����ɼ�ͥ��ҵ�����ʱ�䣬�ڸð���������8��ѧ��������ÿ�������ҵ����ʱ�䣨��λ���֣��ֱ�Ϊ��60��55��75��55��55��43��65��40��
��1�����������ݵ���������λ����
��2������8��ѧ��ÿ����ɼ�ͥ��ҵ��ƽ��ʱ�䣻�������ѧУҪ��ѧ��ÿ����ɼ�ͥ��ҵʱ�䲻�ܳ���60���ӣ��ʸð�ѧ��ÿ����ɼ�ͥ��ҵ��ƽ��ʱ���Ƿ����ѧУ��Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019����ʮ��һ���ƽ����ڼ䣬���ʹ��Ӵ��ο�Լ225000�ˣ���������225000���ÿ�ѧ��������ʾΪ��������
A.225��103B.22.5��104C.2.25��105D.0.225��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������塢Բ����Բ �����ּ������У���һ��ƽ��ֱ�ȥ�����ּ����壬��������״���Խس�������Ҳ���Խس�Բ�εļ�������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���Ķ����⣺
��ͼ�٣�����ABC�У���AB=10��AC=6����BC���ϵ�����AD��ȡֵ��Χ��
�����������������·������ӳ�AD����EʹDE=AD��������BE������ACD���ŵ�D��ʱ����ת180��õ���EBD������AB��AC��2AD��������ABE�У��������������ߵĹ�ϵ�����жϣ�
����AD��ȡֵ��Χ�� ��
��2����������
��ͼ�ڣ�����ABC�У�D��BC���ϵ��е㣬DE��DF�ڵ�D��DE��AB�ڵ�E��DF��AC�ڵ�F������EF����֤��BE+CF��EF��
��3��������չ��
��ͼ�ۣ����ı���ABCD�У���B+��D=180�㣬CB=CD����BCD=140�㣬��Ϊ������һ��70��ǣ��ǵ����߷ֱ�AB��AD��E��F���㣬����EF��̽���߶�BE��DF��EF֮���������ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��һ�κ���y=kx+b��k��bΪ������k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=![]() ��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��nΪ������n��0����ͼ���ڵڶ������ڵ�C��CD��x�ᣬ��ֱΪD����OB=2OA=3OD=6��
��1����һ�κ����뷴���������Ľ���ʽ��
��2����������ͼ�����һ���������ꣻ
��3��ֱ��д������ʽ��kx+b��![]() �Ľ⼯��
�Ľ⼯��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com