练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】两个数的商为正数，则两个数（ ）
    A.都为正
    B.都为负
    C.同号
    D.异号

    【答案】C
    【解析】解：∵两个数的商为正数，

    ∴两个数同号．

    故选C．

    根据有理数的除法结合两个数的商为正数，可得出该两数同号．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

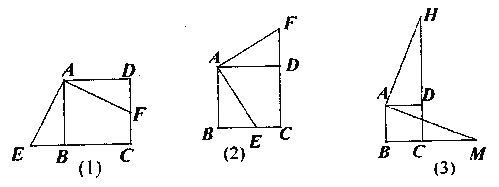
    【题目】(1)观察发现：四边形ABCD是正方形，点E是直线BC上的动点，连结AE,过点A作AF⊥AE交直线CD于F．当点E位于点B的左侧时，如图(1).观察线段AB.BE.CF之间有何数量关系？请直接写出线段AB．BE．CF之间的数量关系．

    (2)拓展探究：当点E位于点B的右侧时，如图（2），线段AB．BE．CF之间有何数量关系？并说明理由.

    (3)迁移应用：如图(3），正方形ABCD的边长为2cm时，线段CM=3cm，直接写出线段CH的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题提出】

    学习了三角形全等的判定方法（即“SSS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    【初步思考】

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    【深入探究】

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据　 　，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是钝角，请你证明：△ABC≌△DEF（提示：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H）．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是锐角，请你利用图③，在图③中用尺规作出△DEF，使△DEF和△ABC不全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知多项式A=（x+1）2﹣（x2﹣4y）．

    （1）化简多项式A；

    （2）若x+2y=1，求A的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）

    A. 3a+2a=6a B. a3a4=a12

    C. a10÷a2=a5 D. （﹣4a4b）2=16a8b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明爸爸经营的水果店出售一种优质热带水果，正在上初三的小明经过调查和计算，发现这种水果每月的销售量y(千克)与销售单价x（元）之间存在着一次函数关系：y=-10x+500(20≤x≤50)．下面是他们的一次对话：

    小明：“您要是告诉我咱家这种水果的进价是多少？我就能帮你预测好多信息呢！”

    爸爸：“咱家这种水果的进价是每千克20元”

    聪明的你，也来解答一下小明想要解决的两个问题：

    （1）若每月获得利润w(元）是销售单价x（元）的函数，求这个函数的表达式．

    （2）当销售单价为多少元时，每月可获得最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若am=3,an=5,a2m+n=________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”，“5”，“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为，按表格要求确定奖项．

    （1）用列表或画树状图的方法求出甲同学获得一等奖的概率；

    （2）是否每次抽奖都会获奖，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O中，直径CD垂直于弦AB，垂足为E，AM⊥BC于点M，交CD于N，连AD.

    （1）求证：AD=AN；

    （2）若AB=，ON=1，求⊙O的半径；

    （3）若且AE=4，求CM的长

    查看答案和解析>>

    同步练习册答案