Question

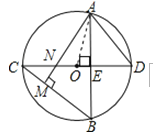
【题目】如图，⊙O中，直径CD垂直于弦AB，垂足为E，AM⊥BC于点M，交CD于N，连AD.

（1）求证：AD=AN；

（2）若AB=，ON=1，求⊙O的半径；

（3）若且AE=4，求CM的长

Answer 1

【答案】（1）证明略 （2）3． （3）CM=2

【解析】试题分析：（1）利用同弧所对的圆周角相等，得出；利用等角的余角相等，得出，利用对顶角相等，等量代换，可得，利用等角对等边，得证.（2）由垂径定理得AE= , 利用NE=DE=x,则OE=x-1,AO=OD=r=2x-1，在 勾股定理，得出x=2,从而解得r=3；（3）由（1）得 ,得 ,相似三角形的面积比等于边长比的平方，则 ,得出CM=2.

试题解析：

（1）

（2）∵AB=，AE⊥CD，∴AE=

又∵ON=1，∴设NE=x，则OE=x-1，NE=ED=x，

r=OD=OE+ED=2x-1

连结AO，则AO=OD=2x-1，
∵△AOE是直角三角形，AE=，OE=x-1，AO=2x-1，
∴

解得x=2，∴r=2x-1=3．

（3）∵AD=AN,AB⊥CD，∴AE平分ND，∴S△ANE=S△ADE

∵S△CMN：S△AND=1:8，∴S△CMN：S△ANE=1:4

又∵△CMN∽△AEN，∴

∵AE=4，∴CM=2