
【题目】如图①,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边的中点.将
边的中点.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角(
角(![]() ),得到
),得到![]() (如图②).
(如图②).



(![]() )
)![]() .
.
(![]() )当
)当![]() 时,
时, ![]() 为直角三角形.
为直角三角形.
(![]() )当
)当![]() 时,旋转角
时,旋转角![]() .
.
(![]() )如图③,在旋转过程中,设
)如图③,在旋转过程中,设![]() 与
与![]() 所在直线交于点
所在直线交于点![]() ,当
,当![]() 成为等腰三角形时,旋转角
成为等腰三角形时,旋转角![]() 或
或![]() ,其中正确的结论有:( ).
,其中正确的结论有:( ).
A. (![]() )(
)(![]() )(
)(![]() ) B. (
) B. (![]() )(
)(![]() )(
)(![]() ) C. (
) C. (![]() )(
)(![]() )(
)(![]() ) D. (
) D. (![]() )(
)(![]() )(
)(![]() )
)
【答案】A
【解析】(1)∵在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边的中点,
边的中点,
∴△ABC和△ADE都是等腰直角三角形,而△AB′C′是由△ABC旋转得到的,
∴易证△ADB′≌△AEC′,
∴DB′=EC′,∠AEC′=∠ADB′,
(2)∵DB′∥AE,
∴∠AED+∠EDB′=180°,
∴∠EDB′=180°-45°=135°,
∴∠ADB′=135°-∠ADE=135°-45°=90°,
∴∠AEC′=∠ADB′=90°,
∴△AEC′是直角三角形;
(3)∵AE=![]() AC=
AC=![]() AC′,∠AEC′=90°,
AC′,∠AEC′=90°,
∴∠AC′E=30°,
∴![]() =∠EAC′=60°;
=∠EAC′=60°;
(4)当△ADP为等腰三角形时,存在以下几种情况:
①当点P在线段DE上,且AD=PD时,∠DAP=∠DBA=![]() ,此时
,此时![]() ;
;
②当点P在线段DE上,且AP=DP时,∠PAD=∠PDA=45°,此时, ![]() ;
;
③当点P在线段DE上,且AP=AD时,∠ADP=∠APD=45°,此时,∠PAD=90°,
∴![]() ,此时点P与点E重合;
,此时点P与点E重合;
④当点P在线段ED的延长线上,且PD=AD时,∠DAP=∠DPA=![]() ∠ADE=22.5°,此时,
∠ADE=22.5°,此时, ![]() =∠PAD+∠DAE=22.5°+90°=112.5°.
=∠PAD+∠DAE=22.5°+90°=112.5°.
综上所述,当△ADP为等腰三角形时, ![]() 的度数为0°或22.5°或45或,112.5°.
的度数为0°或22.5°或45或,112.5°.
即(1)、(2)、(3)是正确的,(4)是错误的;
故选A.


科目:初中数学 来源: 题型:
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”,“5”,“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为![]() ,按表格要求确定奖项.
,按表格要求确定奖项.

(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)是否每次抽奖都会获奖,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
(1)直接写出线段AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD垂直于弦AB,垂足为E,AM⊥BC于点M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径;
,ON=1,求⊙O的半径;
(3)若![]() 且AE=4,求CM的长
且AE=4,求CM的长

查看答案和解析>>
科目:初中数学 来源: 题型:
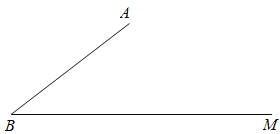
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com