练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若关于x的方程x2﹣kx+4=0有两个相等的实数根，则k的值为 ．

    【答案】k=±4
    【解析】解：∵方程有两个相等的实数根， 而a=1，b=﹣k，c=4，
    ∴△=b2﹣4ac=（﹣k）2﹣4×1×4=0，
    解得k=±4．
    故填：k=±4．
    【考点精析】解答此题的关键在于理解求根公式的相关知识，掌握根的判别式△=b2-4ac，这里可以分为3种情况：1、当△>0时，一元二次方程有2个不相等的实数根2、当△=0时，一元二次方程有2个相同的实数根3、当△<0时，一元二次方程没有实数根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用a、b、c作三角形的三边，其中不能构成直角三角形的是（　　）

    A. a2=（b+c）（b﹣c） B. a：b：c=1： ：2

    C. a=32，b=42，c=52 D. a=5，b=12，c=13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

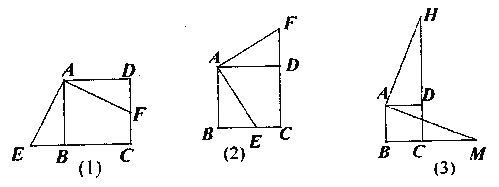
    【题目】(1)观察发现：四边形ABCD是正方形，点E是直线BC上的动点，连结AE,过点A作AF⊥AE交直线CD于F．当点E位于点B的左侧时，如图(1).观察线段AB.BE.CF之间有何数量关系？请直接写出线段AB．BE．CF之间的数量关系．

    (2)拓展探究：当点E位于点B的右侧时，如图（2），线段AB．BE．CF之间有何数量关系？并说明理由.

    (3)迁移应用：如图(3），正方形ABCD的边长为2cm时，线段CM=3cm，直接写出线段CH的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

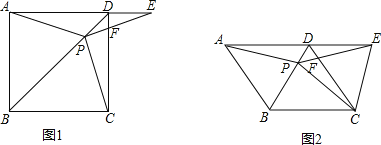
    【题目】如图1在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F.

    （1）证明：PC=PE；

    （2）求∠CPE的度数；

    （3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120度时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点(4，-2)在( )

    A.第一象限B.第二象限C.第三象限D.第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知菱形ABCD，AB＝AC，点E，F分别是BC，AD的中点，连接AE，CF.

    (1)求证：四边形AECF是矩形；

    (2)若AB＝8，求菱形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题提出】

    学习了三角形全等的判定方法（即“SSS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    【初步思考】

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    【深入探究】

    第一种情况：当∠B是直角时，△ABC≌△DEF．

    如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据　 　，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是钝角，请你证明：△ABC≌△DEF（提示：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H）．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是锐角，请你利用图③，在图③中用尺规作出△DEF，使△DEF和△ABC不全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知多项式A=（x+1）2﹣（x2﹣4y）．

    （1）化简多项式A；

    （2）若x+2y=1，求A的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”，“5”，“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为，按表格要求确定奖项．

    （1）用列表或画树状图的方法求出甲同学获得一等奖的概率；

    （2）是否每次抽奖都会获奖，为什么？

    查看答案和解析>>

    同步练习册答案