【题目】用a、b、c作三角形的三边，其中不能构成直角三角形的是（ ）
A. a2=（b+c）（b﹣c） B. a：b：c=1： 
：2
C. a=32，b=42，c=52 D. a=5，b=12，c=13
【答案】C
【解析】试题解析：∵a2=（b+c）（b﹣c），
∴a2=b2﹣c2 ，
∴a2+c2=b2 ，
根据勾股定理的逆定理可得，用a、b、c作三角形的三边，能构成直角三角形，故选项A错误；
∵a：b：c=1： 
：2，
∴设a=x，b=
x，c=2x，
∵
，
∴用a、b、c作三角形的三边，能构成直角三角形，故选项B错误；
∵a=32， b=42， c=52，
∴a2+b2=（32）2+（42）2=81+256=337≠（52）2 ，
∴用a、b、c作三角形的三边，不能构成直角三角形，故选项C正确；
∵a=5，b=12，c=13，
52+122=25+144=169=132 ，
∴用a、b、c作三角形的三边，能构成直角三角形，故选项D错误；
故选C．
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
（1）解方程： 
解：方程化为： 
.
即化为：（2x-3）（x-1）=0，
∴ 2x-3=0或x-1=0，
解得：x=
或x=1.
∴方程的根为： 
， 
.
（2）求解分式方程的过程是：将分式方程化为整式方程，然后求解整式方程，然后将整工方程的根代入验根，舍去增根，得到的根就是原方程的根.
参考上述材料，解决下列问题：
（1）解方程： 
；
（2）若方程
的一个解是x=1，则方程的其他解是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，点P在AD上，AB=2，AP=1．将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF（如图①）．
（1）当点E与点B重合时，点F恰好与点C重合（如图②），求PC的长；
（2）探究：将直尺从图②中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止．在这个过程中，请你观察、猜想，并解答：
①tan∠ PEF的值是否发生变化？请说明理由；
②直接写出从开始到停止，线段EF的中点经过的路线长．
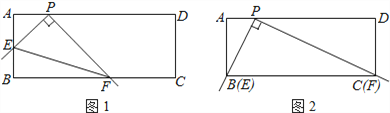
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在□ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．
（1）求证：四边形EHFG是平行四边形；
（2）若四边形EHFG是矩形，则□ABCD应满足的条件是 （不需要证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】□ABCD的对角线的交点在坐标原点，且AD平行于x轴．若点A坐标为(-1，2)，则点C的坐标为（ ）
A. (1，-2) B. (2，-1) C. (1，-3) D. (2，-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
