
����Ŀ���ھ���ABCD�У���P��AD�ϣ�AB=2��AP=1����ֱ�dzߵĶ������P����ֱ�dzߵ����߷ֱ�AB��BC�ڵ�E��F������EF����ͼ������
��1������E���B�غ�ʱ����Fǡ�����C�غϣ���ͼ�ڣ�����PC�ij���
��2��̽������ֱ�ߴ�ͼ���е�λ�ÿ�ʼ���Ƶ�P˳ʱ����ת������E�͵�A�غ�ʱֹͣ������������У�����۲졢���룬�����
��tan�� PEF��ֵ�Ƿ����仯����˵�����ɣ�
��ֱ��д���ӿ�ʼ��ֹͣ���߶�EF���е㾭����·�߳���
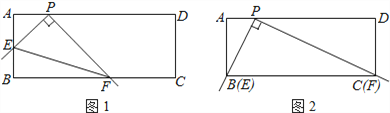
���𰸡���1��PC=2![]() ����2���١�PEF�Ĵ�С���䣮��
����2���١�PEF�Ĵ�С���䣮��![]()
�������������������1���ɹ��ɶ�����PB�����û����ϵ֤����APB�ס�DCP���������Ʊ���PC��
��2����tan��PEF��ֵ���䣮��F��FG��AD������ΪG��ͬ��1���ķ���֤����APB�ס�DCP�������Ʊ�![]() =2��������������Ǻ����Ķ�����ֵ��
=2��������������Ǻ����Ķ�����ֵ��
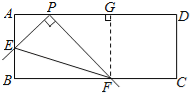
����ͼ3��������ʼλ�ú��յ�λ��ʱ���߶�EF���е�O1��O2������O1O2���߶�O1O2��Ϊ�߶�EF���е㾭����·�߳���Ҳ������BPC����λ�ߣ�
�����������1���ھ���ABCD�У���A=��D=90����
AP=1��CD=AB=2����PB=![]() ��
��
���ABP+��APB=90����
���ߡ�BPC=90����
���APB+��DPC=90����
���ABP=��DPC��
���APB�ס�DCP��
��![]() ����
����![]() ��
��
��PC=2![]() ��
��
��2����tan��PEF��ֵ���䣮
���ɣ���F��FG��AD������ΪG��
���ı���ABFG�Ǿ��Σ�
���A=��PGF=90����GF=AB=2��
���AEP+��APE=90����
���ߡ�EPF=90����
���APE+��GPF=90����
���AEP=��GPF��
���APE�ס�GPF��
��![]() =2��
=2��
��Rt��EPF��tan��PEF=![]() =2��
=2��
��tan��PEF��ֵ���䣻
�����߶�EF���е�ΪO������OP��OB��
����Rt��EPF��OP=![]() EF��
EF��
��Rt��EBF��OB=![]() EF��
EF��
��OP=OB=![]() EF��
EF��
��O�����߶�BP�Ĵ�ֱƽ�����ϣ�
���߶�EF���е㾭����·�߳�ΪO1O2=![]() PC=
PC=![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У���ȷ���ǣ�������
A.a2a3��a5B.��a2��3��a5C.a6��a2��a3D.a5+a5��a10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��1����2������y��ԳƵĵ�������ǣ�������
A. ����1����2�� B. ��1��2�� C. ����1��2�� D. ����2��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��2��3����B��3��1����C����2����2�������ڸ���ϣ�

��1��������ABC����y��ԳƵġ�A1B1C1��
��2��ֱ��д����ABC����x��ԳƵġ�A2B2C2�ĸ������ꣻ
��3�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˽�һ�����⽻ͨӵ�����⣬������һ����Ϊ7ǧ�Ĺ�·�����ƽ��ÿ�������y����Ԫ����������x���죩��30��x��12 0֮��ʱ����һ�κ����Ĺ�ϵ�����±���ʾ��

��1����y����x�ĺ�����ϵʽ��
��2�����������Ĺ����мƻ������ı䣬������������3ǧ�ף������û��������������������£���������·�ȼƻ�����15�죬��ԭ�ƻ�ÿ������ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��c�������ε����ߣ����в��ܹ���ֱ�������ε��ǣ�������
A. a2=��b+c����b��c�� B. a��b��c=1�� ![]() ��2
��2
C. a=32��b=42��c=52 D. a=5��b=12��c=13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
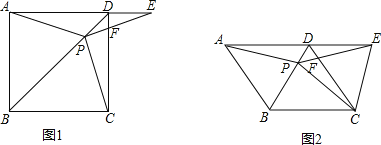
����Ŀ����ͼ1��������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F.
��1��֤����PC=PE��
��2�����CPE�Ķ�����
��3����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ������CE����̽���߶�AP���߶�CE��������ϵ����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com