
【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.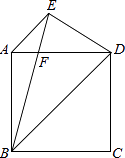
【答案】证明:连接AC,交BD于点O,作EG⊥BD于点G.
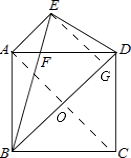
∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO= ![]() AC=
AC= ![]() BD=
BD= ![]() BE,
BE,
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
【解析】连接AC,交BD于点O,作EG⊥BD垂足为G,先证明四边形AOGE是矩形,从而可得到EG=![]() BD=
BD=![]() BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你填空:
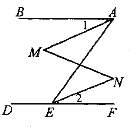
解:∵∠BAE+∠AED=180° (已知) ,
∴AB//DE( ),
∴∠BAE= ( )
又 ∵∠1=∠2(已知)
∴∠BAE-∠1= - (等式性质),
即∠MAE=∠NEA,
∴ ∥ ( ),
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
(1)若AC=9cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形AOBC是矩形,以O为坐标原点,OB、OA分别在x轴、y轴上,点A的坐标为(0,3),∠OAB=60°,以AB为轴对折后,C点落在D点处,则D点的坐标为( )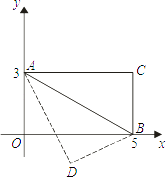
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,点B2013的坐标为( )

A. (42012×![]() ,42012) B. (24026×
,42012) B. (24026×![]() ,24026) C. (24026×
,24026) C. (24026×![]() ,24024) D. (44024×
,24024) D. (44024×![]() ,44024)
,44024)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数图象经过(-4,-9)和(3,5)两点.
①求一次函数解析式.
②求图象和坐标轴交点坐标.并画出图象.
③求图象和坐标轴围成三角形面积.
④若点(2,a)在函数图象上,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com