
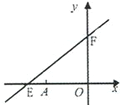
【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
【答案】(1)![]() ;(2)S
;(2)S![]() x+18 (-8<x<0);(3)(-4,3).
x+18 (-8<x<0);(3)(-4,3).
【解析】
(1)将点E坐标(﹣8,0)代入直线y=kx+6就可以求出k值;
(2)先求出函数的解析式,再由点A的坐标为(﹣6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为9代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,∴0=﹣8k+6,∴k![]() ;
;
(2)∵k![]() ,∴直线的解析式为:y
,∴直线的解析式为:y![]() x+6.
x+6.
∵P点在y![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),∴△OPA以OA为底的边上的高是|
x+6),∴△OPA以OA为底的边上的高是|![]() x+6|,当点P在第二象限时,|
x+6|,当点P在第二象限时,|![]() x+6|
x+6|![]() x+6.
x+6.
∵点A的坐标为(﹣6,0),∴OA=6,∴S![]() x+18.
x+18.
∵P点在第二象限,∴﹣8<x<0;∴S![]() x+18 (-8<x<0);
x+18 (-8<x<0);
(3)设点P(x,y)时,其面积S![]() 9,则
9,则![]() x+18=9,解得:x=-4.
x+18=9,解得:x=-4.
∵P点在y![]() x+6上,∴y
x+6上,∴y![]() ×(-4)+6=3,故P(-4,3).
×(-4)+6=3,故P(-4,3).
所以,P(-4,3)时,三角形OPA的面积为9.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠C=60°,D,E分别是边AB,BC上两点,且DE∥AC,下列结论不正确的是( )
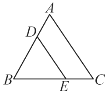
A. ∠A=60° B. △BDE是等腰三角形 C. BD≠DE D. △BDE是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B,C开始,以相同的速度中⊙O上逆时针运动.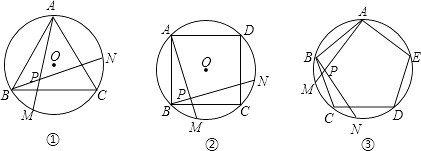
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 , 图③中∠APB的度数是;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】内部员工互相交换职位是公司培养新人的一种模式,如图1,位于成都的某集团总公司在距离成都![]() 的
的![]() 市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从
市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从![]() 市出发,并以各自的速度匀速行驶,小王到达中途的
市出发,并以各自的速度匀速行驶,小王到达中途的![]() 地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达
地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达![]() 市,结果两人同时到达
市,结果两人同时到达![]() 市.小颖和小王距各自出发地的路程
市.小颖和小王距各自出发地的路程![]() (千米)与小王开车出发所用的时间
(千米)与小王开车出发所用的时间![]() (小时)的关系如图2,结合图象信息解答下列问题:
(小时)的关系如图2,结合图象信息解答下列问题:
(1)小颖的速度是____________千米/时,图2中![]() ____________;小王的速度是____________千米/时;
____________;小王的速度是____________千米/时;
(2)请写出小王距他的出发地![]() 市的距离
市的距离![]() 与他出发的时间
与他出发的时间![]() 的关系式;
的关系式;
(3)直接写出小颖和小王相距100千米时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )

A. 6B. 12C. 4D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题: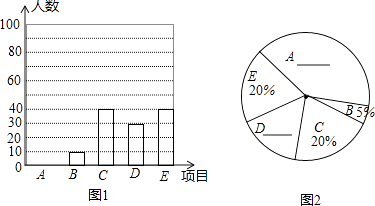
(1)在这项调查中,共调查了名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
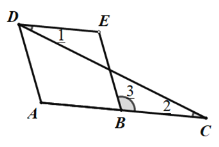
【题目】如图: 下面是一道证明题,刘老师给同学们讲解了思路,请将证明过程和每一步的理由补充完整.
已知:∠A=∠E,AD∥BE,求证:∠1=∠2
证明:![]() AD∥BE(已知)
AD∥BE(已知)
∠A= ( )
![]() ∠A=∠E ( 已知 )
∠A=∠E ( 已知 )
![]() ∠E= (等量代换)
∠E= (等量代换)
![]() DE∥AC( )
DE∥AC( )
![]() ∠1=∠2( )
∠1=∠2( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
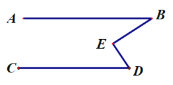
证明如下:过E点作EF∥AB.
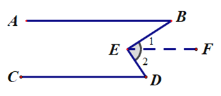
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
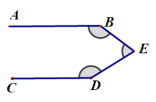
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
[创新应用]:
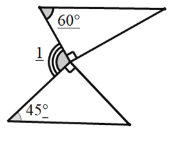
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
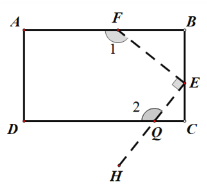
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过(﹣2,0),则下列结论:①bc>0;②b+2a=0;③a+c>b;④16a+4b+c=0;⑤3a+c<0,其中正确结论的个数是( )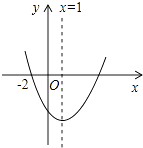
A.5
B.4
C.3
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com