
����Ŀ���ڲ�Ա�����ཻ��ְλ�ǹ�˾�������˵�һ��ģʽ����ͼ1��λ�ڳɶ���ij�����ܹ�˾�ھ���ɶ�![]() ��
��![]() ������һ���ֹ�˾���ֶ�����ְ1����ܹ�˾Сӱ�ͷֹ�˾С����ְλ����ѧϰ����������Сӱ�����ӳɶ�������1��Сʱ��С��������
������һ���ֹ�˾���ֶ�����ְ1����ܹ�˾Сӱ�ͷֹ�˾С����ְλ����ѧϰ����������Сӱ�����ӳɶ�������1��Сʱ��С��������![]() �г��������Ը��Ե��ٶ�������ʻ��С��������;��
�г��������Ը��Ե��ٶ�������ʻ��С��������;��![]() ��ʱͻȻ�ӵ��ֹ�˾����ֻ֪ͨ��ԭ·ԭ�ٷ��أ���Сӱ����һֱ�ӳɶ�ֱ��
��ʱͻȻ�ӵ��ֹ�˾����ֻ֪ͨ��ԭ·ԭ�ٷ��أ���Сӱ����һֱ�ӳɶ�ֱ��![]() �У��������ͬʱ����
�У��������ͬʱ����![]() �У�Сӱ��С������Գ����ص�·��
�У�Сӱ��С������Գ����ص�·��![]() (ǧ��)��С�������������õ�ʱ��
(ǧ��)��С�������������õ�ʱ��![]() (Сʱ)�Ĺ�ϵ��ͼ2�����ͼ����Ϣ����������⣺
(Сʱ)�Ĺ�ϵ��ͼ2�����ͼ����Ϣ����������⣺
��1��Сӱ���ٶ���____________ǧ��/ʱ��ͼ2��![]() ____________��С�����ٶ���____________ǧ��/ʱ��
____________��С�����ٶ���____________ǧ��/ʱ��
��2����д��С�������ij�����![]() �еľ���
�еľ���![]() ����������ʱ��
����������ʱ��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��3��ֱ��д��Сӱ��С�����100ǧ��ʱ![]() ��ֵ��
��ֵ��

���𰸡���1��60��7��100����2��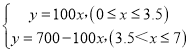 ����3��2��
����3��2��![]() ��
��![]()
��������
��1����x=0ʱ��Сӱ��y=60����Сӱ���ٶ�Ϊ60km/h��ͨ������Сӱȫ����Ҫ��ʱ��ɵ�a��С�����ص�·�̳�ʱ��õ�С�����ٶȣ�
��2��С���Ĺ�ϵʽ��Ҫ��2�Σ�һ����С����ɶ�������һ���Ƿ��أ�
��3������3�������һ����С����Сӱδ���������100km��һ����������������������ǰ�ߣ����100km������һ����С�����غ���Сӱ������Ϊ100km
��1����x=0ʱ��Сӱ��y=60����Сӱ���ٶ�Ϊ60km/h
��ͼ��ã���·��Ϊ480km
��a=![]()
��С����Сӱһ��A������С������һ�˵�ʱ��ҲΪ7h
��ͼ��ã�С������ʻ��350km��
��С������һ�˵��ܾ���Ϊ700km
��С�����ٶ�Ϊ��![]() km/h
km/h
��2�����һ��С����ɶ�����
��y=100x��(0��x��3.5)
�������������A��
��y=350��100(x��3.5)=700��100x��![]()
��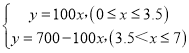
��3�����һ������ͼ����Сӱ��С�������������δ����ʱ����![]() ʱ�����100km
ʱ�����100km

��![]()
�����������ͼ��Сӱ��С������������У�ֱ��������������ǰ������![]() ʱ�����100km
ʱ�����100km

��![]()
�����������ͼ��Сӱ����ǰ����С���۷���A��ʻ��С����Сӱ����![]() ʱ�����100km
ʱ�����100km

480��60��60![]()
��ã�![]()
���ϵã�t=2��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A��0��8������B��6��8����
��1��ֻ��ֱ�ߣ�û�п̶ȣ���Բ�棬����һ����P��ʹ��Pͬʱ������������������Ҫ������ͼ�ۼ�������д����������
�ٵ�P��A��B����ľ�����ȣ�
�ڵ�P����xOy�����ߵľ�����ȣ�
��2���ڣ�1��������P��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB=a��BC=b��a��2b������P�ڱ�CD�ϣ���PC=BC��������ABCD�Ƶ�P˳ʱ����ת90����õ�������A'B'C'D'����B'��C'���ڱ�AB�ϣ�������a��b�Ĵ���ʽ�ֱ��ʾ����ͼ�ε������
��1��������PCC'�����S1��
��2���ı���AA'CC'�����S��������
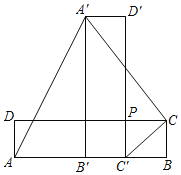
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��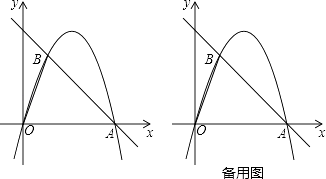
��1����a��b��ֵ��
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£���S��ACN=S��PMNʱ������ON����Q���߶�BP�ϣ�����Q��QR��MN��ON�ڵ�R������MQ��BR������MQR����BRN=45��ʱ�����R�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���е�.
a��ԭ�ı���ABCD�ĶԽ���AC��BD����________ʱ���ı���EFGH�Ǿ��Σ�
b��ԭ�ı���ABCD�ĶԽ���AC��BD����________ʱ���ı���EFGH�����Σ�
c��ԭ�ı���ABCD�ĶԽ���AC��BD����________ʱ���ı���EFGH�������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,С�ԴӼ�(��0)����,���ŵ���������A0B�ı�0A-AB-B0��·��ȥ������ɢ��,����0A=0B����С�Ծ��(��0)�ľ���ΪS,ɢ����ʱ��Ϊt,������ͼ�����ܴ��¿̻�S��t֮�亯����ϵ��ͼ���ǣ� ��

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
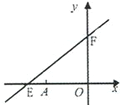
����Ŀ����ͼ��ֱ��y=kx+6��x�ᡢy��ֱ���E��F����E����Ϊ(-8��0)����A������Ϊ(-6��0)��
��1����k��ֵ��
��2������P(x��y)�ǵڶ������ڵ�ֱ���ϵ�һ�����㣬����P�˶������У���д��������OPA�����S��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��̽������P�˶���ʲôλ��ʱ��������OPA�����Ϊ9����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��AB��ֱ������C���������AB���ӳ��߽���P�㣬����P=40�㣬���D�Ķ���Ϊ �� 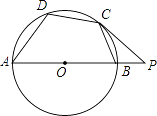
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
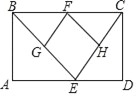
����Ŀ����֪����ABCD�У�E��AD���ϵ�һ�����㣬��F��G��H�ֱ���BC��BE��CE���е㣮
��1����֤����BGF�ա�FHC��
��2����AD=a�����ı���EGFH��������ʱ�������ABCD�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com