
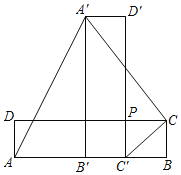
【题目】如图,在长方形ABCD中,AB=a,BC=b(a>2b),点P在边CD上,且PC=BC,长方形ABCD绕点P顺时针旋转90°后得到长方形A'B'C'D'(点B'、C'落在边AB上),请用a、b的代数式分别表示下列图形的面积.
(1)三角形PCC'的面积S1;
(2)四边形AA'CC'的面积S,并化简.
【答案】(1)△PCC'的面积S1=![]() b2;(2)
b2;(2)![]() +
+![]()
【解析】
(1)依据△PCC'是等腰直角三角形,即可得出△PCC'的面积S1=![]() b2;
b2;
(2)依据△BCC'是等腰直角三角形,可得BC'=BC=b,BB'=2b,进而得到AB'=a-2b,再根据四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'进行计算即可.
(1)由旋转可得,PC=PC'=b,∠CPC'=90°,

∴△PCC'是等腰直角三角形,
∴△PCC'的面积S1=![]() b2;
b2;
(2)由题可得,∠BCC'=45°,∠B=90°,A'B'=AB=a,
∴∠BCC'=∠BC'C=45°,
∴△BCC'是等腰直角三角形,
∴BC'=BC=b,BB'=2b,
∴AB'=a-b-b=a-2b,
∴四边形AA'CC'的面积S=S△AB'A'+S梯形A'B'BC-S△BCC'
=![]() a(a-2b)+
a(a-2b)+![]() -
-![]()
=![]() -ab+ab+b2-
-ab+ab+b2-![]()
=![]() +
+![]() .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线![]() ,则直线
,则直线![]() 与
与![]() 平行.
平行.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠C=60°,D,E分别是边AB,BC上两点,且DE∥AC,下列结论不正确的是( )
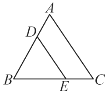
A. ∠A=60° B. △BDE是等腰三角形 C. BD≠DE D. △BDE是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于点D,交AB于点E,CD=2,则AC等于( )
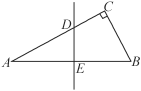
A. 4 B. 5 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了增强学生对中华优秀传统文化的理解,决定购买一批相关的书籍.据了解,经典著作的单价比传说故事的单价多6元,用10000元购买经典著作与用7000元购买传说故事的本数相同,这两类书籍的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举办“大爱镇江”征文活动,小明为此次活动设计了一个以三座山为背景的图标(如图),现用红、黄两种颜色对图标中的A、B、C三块三角形区域分别涂色,一块区域只涂一种颜色.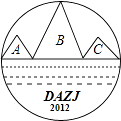
(1)请用树状图列出所有涂色的可能结果;
(2)求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B,C开始,以相同的速度中⊙O上逆时针运动.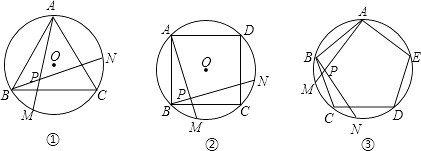
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 , 图③中∠APB的度数是;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】内部员工互相交换职位是公司培养新人的一种模式,如图1,位于成都的某集团总公司在距离成都![]() 的
的![]() 市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从
市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从![]() 市出发,并以各自的速度匀速行驶,小王到达中途的
市出发,并以各自的速度匀速行驶,小王到达中途的![]() 地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达
地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达![]() 市,结果两人同时到达
市,结果两人同时到达![]() 市.小颖和小王距各自出发地的路程
市.小颖和小王距各自出发地的路程![]() (千米)与小王开车出发所用的时间
(千米)与小王开车出发所用的时间![]() (小时)的关系如图2,结合图象信息解答下列问题:
(小时)的关系如图2,结合图象信息解答下列问题:
(1)小颖的速度是____________千米/时,图2中![]() ____________;小王的速度是____________千米/时;
____________;小王的速度是____________千米/时;
(2)请写出小王距他的出发地![]() 市的距离
市的距离![]() 与他出发的时间
与他出发的时间![]() 的关系式;
的关系式;
(3)直接写出小颖和小王相距100千米时![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[感知发现]:如图,是一个“猪手”图,AB∥CD,点E在两平行线之间,连接BE,DE ,我们发现:∠E=∠B+∠D
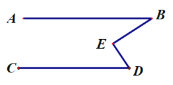
证明如下:过E点作EF∥AB.
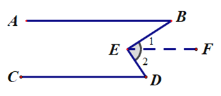
![]() ∠B=∠1(两直线平行,内错角相等.)
∠B=∠1(两直线平行,内错角相等.)
又![]() AB∥CD(已知)
AB∥CD(已知)
![]() CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行.)
![]() ∠2=∠D(两直线平行,内错角相等.)
∠2=∠D(两直线平行,内错角相等.)
![]() ∠1+∠2=∠B+∠D(等式的性质1.)
∠1+∠2=∠B+∠D(等式的性质1.)
即:∠E=∠B+∠D
[类比探究]:如图是一个“子弹头”图,AB∥CD,点E在两平行线之间,连接BE,DE.试探究∠E+∠B+∠D=360°.写出证明过程.
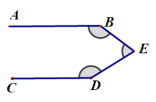
[创新应用]:
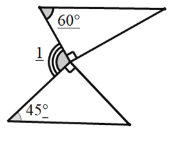
(1).如图一,是两块三角板按如图所示的方式摆放,使直角顶点重合,斜边平行,请直接写出∠1的度数.
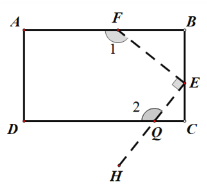
(2).如图二,将一个长方形ABCD按如图的虚线剪下,使∠1=120![]() ,∠FEQ=90°. 请直接写出∠2的度数.
,∠FEQ=90°. 请直接写出∠2的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com