
【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.
【答案】(1)![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元;(2)租地方案有4种,具体方案详见解析;(3)种植
元;(2)租地方案有4种,具体方案详见解析;(3)种植![]() 类蔬菜的面积为11亩,种植
类蔬菜的面积为11亩,种植![]() 类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
【解析】
(1)设![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元,再根据甲、乙种植户的总收入建立二元一次方程组,然后解方程组即可;
元,再根据甲、乙种植户的总收入建立二元一次方程组,然后解方程组即可;
(2)结合(1)的结论,建立不等式组,然后求出其正整数解即可;
(3)设总收入为![]() 元,根据题(2)可得
元,根据题(2)可得![]() 与a的函数关系式,再根据一次函数的性质求解即可.
与a的函数关系式,再根据一次函数的性质求解即可.
(1)设![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元
元
由题意得:![]()
解得![]()
答:![]() 两类蔬菜每亩平均收入分别是
两类蔬菜每亩平均收入分别是![]() 元,
元,![]() 元;
元;
(2)设用来种植![]() 类蔬菜的面积
类蔬菜的面积![]() 亩,则用来种植
亩,则用来种植![]() 类蔬菜的面积为
类蔬菜的面积为![]() 亩,其中a为整数
亩,其中a为整数
由题意得: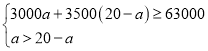
解得![]()
![]() 为整数
为整数
![]() a的取值为
a的取值为![]()
因此,租地方案有以下4个:
类别 | 种植面积单位: (亩) | |||
|
|
|
|
|
B |
|
|
|
|
(3)设总收入为![]() 元
元
由(2)可得:![]()
由一次函数的性质可知,当![]() 时,
时,![]() 随a的增大而减小
随a的增大而减小
则(2)中的4个方案中,当![]() 时,总收入
时,总收入![]() 最大,最大值为
最大,最大值为![]() (元)
(元)
答:种植![]() 类蔬菜的面积为11亩,种植
类蔬菜的面积为11亩,种植![]() 类蔬菜的面积为9亩时,总收入最大,最大值为64500元.
类蔬菜的面积为9亩时,总收入最大,最大值为64500元.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的3月15日是“国际消费者权益日”,许多家居商城都会利用这个契机进行打折促销活动.甲卖家的A商品成本为600元,在标价1000元的基础上打8折销售.
(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于20%?
(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A商品,其成本、标价与甲卖家一致,以前每周可售出50件,现乙卖家先将标价提高2m%,再大幅降价24m元,使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 ![]() m%,这样一天的利润达到了20000元,求m的值.
m%,这样一天的利润达到了20000元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
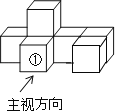
A. 主视图不变,左视图不变
B. 左视图改变,俯视图改变
C. 主视图改变,俯视图改变
D. 俯视图不变,左视图改变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿着矩形的边顺时针方向运动一周回到点
出发,沿着矩形的边顺时针方向运动一周回到点![]() ,则点
,则点![]() 围成的图形面积
围成的图形面积![]() 与点
与点![]() 运动路程
运动路程![]() 之间形成的函数关系式的大致图象是( )
之间形成的函数关系式的大致图象是( )
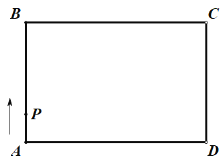
A.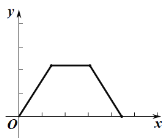 B.
B.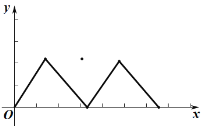
C.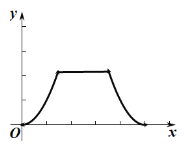 D.
D.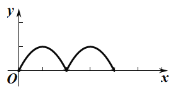
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (
(![]() 为常数,
为常数,![]() )的图象过点
)的图象过点![]() 和点
和点![]() ,函数图象最低点
,函数图象最低点![]() 的纵坐标为
的纵坐标为![]() .直线
.直线![]() 的解析式为
的解析式为![]()
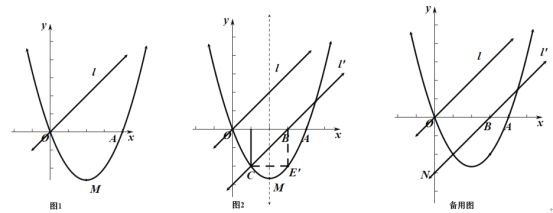
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 直线
直线![]() 沿
沿![]() 轴向右平移,得直线
轴向右平移,得直线![]() ,
,![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与
,与![]() 轴下方的抛物线相交于点
轴下方的抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,把
,把![]() 沿直线
沿直线![]() 折叠,当点
折叠,当点![]() 恰好落在抛物线上点
恰好落在抛物线上点![]() 时(图
时(图![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,
的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,P为
,P为![]() 上的动点,当
上的动点,当![]() 为等腰三角形时,求符合条件的点
为等腰三角形时,求符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地让学生适应中考体育:“1分钟跳绳”项目,对全校九年级200名学生进行了“1分钟跳绳”的测试,现随机抽取20名学生成绩进行分析,过程如下:
收集数据 20名学生的“1分钟跳绳”成绩(单位:个)如下
110 125 134 135 115 146 148 124 153 145
157 160 162 162 165 168 172 128 137 130
整理数据 请你按如下表格分组整理、描述样本数据,并把下列表格补充完整.(说明:每分钟跳绳个数达到160个及以上得满分)
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
人数 |
成绩 |
|
|
等级 |
|
|
人数 |
分析数据 请将下列表格补充完整:
平均数 | 中位数 | 满分率 |
143.8 | 30% |
得出结论
(1)用样本中的统计量估计全校九年级学生“1分钟跳绳”等级为__________;
(2)估计该校九年级200名学生中测试“1分钟跳绳”等级为![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
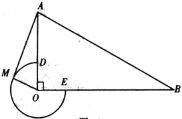
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
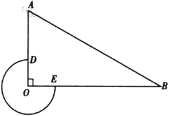
备用图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com