
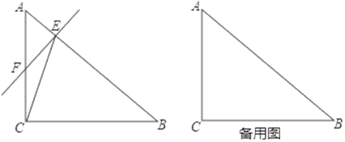
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点E从点A出发沿着线段AB向终点B运动,速度为每秒3个单位长度,过点E作EF⊥AB交直线AC于点F,连结CE.设点E的运动时间为t秒.
(1)当点F在线段AC上(不含端点)时,
①求证:△ABC∽△AFE;
②当t为何值时,△CEF的面积为1.2;
(2)在运动过程中,是否存在某时刻t,使△CEF为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)①见解析;②![]() 秒或1秒;(2)存在,
秒或1秒;(2)存在,![]() 秒或
秒或![]() 秒
秒
【解析】
(1)①根据相似三角形的判定解答即可;
②过点 C 作 CH⊥AB 于 H,利用相似三角形的性质和三角形面积公式解答即可;
(2)根据等腰三角形的判定分两种情况解答.
解:(1)当点 F 在线段 AC 上时,
①证明如下:∵EF⊥AB,
∴∠AEF=90°
在△ABC 中,∠ACB=90°
∴∠ACB=∠AEF 又∵∠A=∠A
∴△ABC∽△AFE
②当 t 秒时,AE=3t, 由①得△ABC∽△AFE
∴![]() ,即
,即![]() ,
,
∴FE=4t
在 Rt△ABC 中,AB=![]()
![]() ,
,
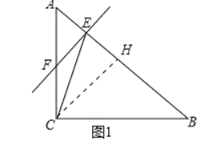
过点 C 作 CH⊥AB 于 H,如图 1:
由面积法可得:![]()
∴![]()
∴![]()
=![]()
![]() .
.
令![]() ,
,
解得:![]() ,
,
经检验,符合题意.
答:当 t 为![]() 秒或 1 秒时,△CEF 的面积为 1.2.
秒或 1 秒时,△CEF 的面积为 1.2.
(2)存在,理由如下:
i)当点 F 在线段 AC 上时(0<t<![]() ),
),
∵∠CFE=∠AEF+∠A>90°,
∴当△CEF 为等腰三角形时,只能是 FC=FE,
由②可知:FE=4t,
∴AF=5t,FC=4t,
∴5t+4t=6,
∴t=![]() .
.
ii)当点 F 在线段 AC 的延长线上时(![]() <t
<t![]() ),如图 2,
),如图 2,
∵∠FCE=∠FCB+∠ECB>90°,
∴当△CEF 为等腰三角形时,只能是 FC=EC,
此时∠F=∠CEF,
∵EF⊥AB,
∴∠AEF=90°,即∠CEA+∠CEF=90°, 又∠F+∠A=90°
∴∠CEA=∠A,
∴CE=AC=6,
∴FC=6,
∴AF=12, 即 5t=12
∴![]()
综上所述,t 的值为![]() 秒或
秒或![]() 秒时,△CEF 为等腰三角形.
秒时,△CEF 为等腰三角形.



 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
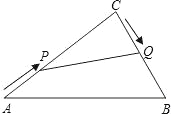
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.
(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以点C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
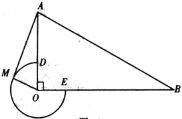
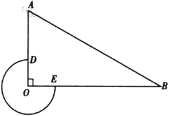
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
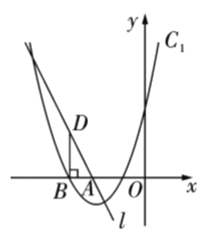
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 作
作![]() 垂直
垂直![]() 轴交直线
轴交直线![]() 于点
于点![]() .
.
(1)求抛物线的函数表达式;
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]()
①求点![]() 的坐标;
的坐标;
②将拋物线![]() 向右平移使它经过点
向右平移使它经过点![]() ,此时得到的抛物线记为
,此时得到的抛物线记为![]() ,求出抛物线
,求出抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com