
【题目】在⊙O中直径为4,弦AB=2![]() ,点C是圆上不同于A、B的点,那么∠ACB度数为_____.
,点C是圆上不同于A、B的点,那么∠ACB度数为_____.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
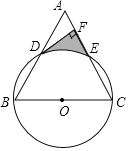
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 和四边形
和四边形![]() 都是平行四边形,点
都是平行四边形,点![]() 为
为![]() 的中点,
的中点,![]() 分别交
分别交![]() 于点
于点![]() ,平行四边形
,平行四边形![]() 的面积为 6,则图中阴影部分的面积为___________ .
的面积为 6,则图中阴影部分的面积为___________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,且
重合)点,且![]() 于
于![]() 相交于点
相交于点![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)当![]() 时,证明:
时,证明:![]() .
.
(3)![]() 面积的最小值是_______.
面积的最小值是_______.
(4)当![]() 的内心在
的内心在![]() 的外部时,直接写出
的外部时,直接写出![]() 的范围______.
的范围______.
查看答案和解析>>
科目:初中数学 来源: 题型:
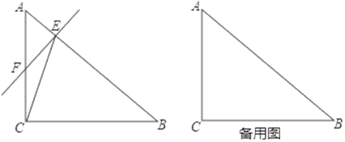
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8,动点E从点A出发沿着线段AB向终点B运动,速度为每秒3个单位长度,过点E作EF⊥AB交直线AC于点F,连结CE.设点E的运动时间为t秒.
(1)当点F在线段AC上(不含端点)时,
①求证:△ABC∽△AFE;
②当t为何值时,△CEF的面积为1.2;
(2)在运动过程中,是否存在某时刻t,使△CEF为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是![]() 元
元![]() 台经过市场销售后发现:在一个月内,当售价是
台经过市场销售后发现:在一个月内,当售价是![]() 元
元![]() 台时,可售出
台时,可售出![]() 台,且售价每降低
台,且售价每降低![]() 元,就可多售出
元,就可多售出![]() 台.若供货商规定这种空气净化器售价不能低于
台.若供货商规定这种空气净化器售价不能低于![]() 元
元![]() 台,代理销售商每月要完成不低于
台,代理销售商每月要完成不低于![]() 台的销售任务.
台的销售任务.
(1)试确定月销售量![]() (台)与售价
(台)与售价![]() (元
(元![]() 台)之间的函数关系式;
台)之间的函数关系式;
(2)求售价![]() 的范围;
的范围;
(3)当售价![]() (元
(元![]() 台)定为多少时,商场每月销售这种空气净化器所获得的利润
台)定为多少时,商场每月销售这种空气净化器所获得的利润![]() (元)最大?最大利润是多少?
(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
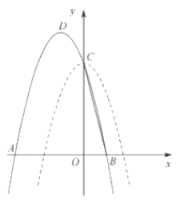
【题目】如图,将抛物线![]() 平移后,新抛物线经过原抛物线的顶点
平移后,新抛物线经过原抛物线的顶点![]() ,新抛物线与
,新抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,联结
,联结![]() ,
,![]() ,设新抛物线与
,设新抛物线与![]() 轴的另一交点是
轴的另一交点是![]() ,新抛物线的顶点是
,新抛物线的顶点是![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设点![]() 在新抛物线上,联结
在新抛物线上,联结![]() ,如果
,如果![]() 平分
平分![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,将抛物线![]() 沿
沿![]() 轴左右平移,点
轴左右平移,点![]() 的对应点为
的对应点为![]() ,当
,当![]() 和
和![]() 相似时,请直接写出平移后得到抛物线的表达式.
相似时,请直接写出平移后得到抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com