
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
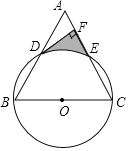
【答案】(1)证明见解析;(2)![]()
【解析】(1)连接CD、OD,先利用等腰三角形的性质证AD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得;
(2)连接OE、作OG⊥AC,求出EF、DF的长及∠DOE的度数,根据阴影部分面积=S梯形EFDO-S扇形DOE计算可得.
(1)如图,连接CD、OD,
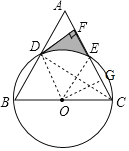
∵BC是⊙O的直径,
∴∠CDB=90°,即CD⊥AB,
又∵△ABC是等边三角形,
∴AD=BD,
∵BO=CO,
∴DO是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE、作OG⊥AC于点G,
∴∠OGF=∠DFG=∠ODF=90°,
∴四边形OGFD是矩形,
∴FG=OD=4,
∵OC=OE=OD=OB,且∠COE=∠B=60°,
∴△OBD和△OCE均为等边三角形,
∴∠BOD=∠COE=60°,CE=OC=4,
∴EG=![]() CE=2、DF=OG=OCsin60°=2
CE=2、DF=OG=OCsin60°=2![]() ,∠DOE=60°,
,∠DOE=60°,
∴EF=FG-EG=2,
则阴影部分面积为S梯形EFDO-S扇形DOE
=![]() ×(2+4)×2
×(2+4)×2![]() -
-![]()
=![]() .
.


科目:初中数学 来源: 题型:
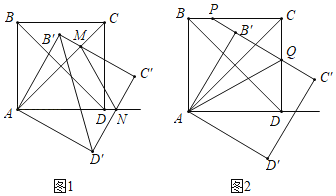
【题目】如图将正方形ABCD绕点A顺时针旋转角度α(0°<α<90°)得到正方形AB′C′D′.
(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α;
(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α=30°时.
①求∠DAQ的度数;
②若AB=6,求PQ的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
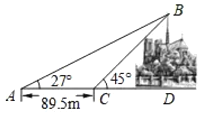
【题目】当地时间2019年4月15日下午,法国巴黎圣母院发生火灾,大火烧毁了巴黎圣母院后塔的塔顶.烧毁前,为测量此塔顶![]() 的高度,在地面选取了与塔底
的高度,在地面选取了与塔底![]() 共线的两点
共线的两点![]() 、
、![]() ,
,![]() 、
、![]() 在
在![]() 的同侧,在
的同侧,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为27°,在
的仰角为27°,在![]() 处测量塔顶
处测量塔顶![]() 的仰角为45°,
的仰角为45°,![]() 到
到![]() 的距离是89.5米.设
的距离是89.5米.设![]() 的长为
的长为![]() 米,则下列关系式正确的是( )
米,则下列关系式正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
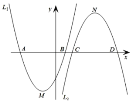
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第三象限的双曲线
在第三象限的双曲线![]() 上,过点
上,过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() ,连接
,连接![]() ,则
,则![]() 的面积为__________.
的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
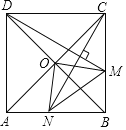
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子内有![]() 颗相同的球,将
颗相同的球,将![]() 颗球分别标示号码
颗球分别标示号码![]() ,
,![]() ,
,![]() ,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球
,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球![]() 次,现已取了
次,现已取了![]() 次,取出的号码依次为
次,取出的号码依次为![]() ,
,![]() ,
,![]() ,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球
,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球![]() 次,则发生“这
次,则发生“这![]() 次得分的平均数在
次得分的平均数在![]() 之间(含
之间(含![]() ,
,![]() )”的情形的概率为________.
)”的情形的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
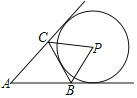
A.8B.10C.13D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com