
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
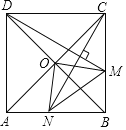
A.①②③B.①③④C.①②④D.②③④
【答案】A
【解析】
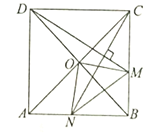
根据正方形的性质,依次判定△CNB≌△DMC,△AON≌△BOM,△OCM≌△OBN,![]() ,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
,根据全等三角形的性质以及勾股定理进行计算即可得出结论.
∵正方形ABCD中,CD=BC,∠BCD=90![]() ,
,
∴∠BCN+∠DCN=90![]() ,
,
又∵CN⊥DM,
∴∠CDM+∠DCN=90![]() ,
,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90![]() ,
,
∴△CNB≌△DMC(ASA),
∴BN=CM,
故AN=BM
∵AO=BO,∠OAN=∠OBM=45°,
∴△AON≌△BOM,
∵BO=CO,∠OCM=∠OBN =45°,
∴△OCM≌△OBN,
∴![]() =S△OBN+ S△BOM= S△OBN+S△AON=S△AOB=
=S△OBN+ S△BOM= S△OBN+S△AON=S△AOB=![]()
![]()
即![]() ,①正确;
,①正确;
∵△AON≌△BOM,
∵∠MON=∠BOM+∠BON=∠AON +∠BON=90°,ON=OM
∴△MNO是等腰直角三角形,
∴MN=![]()
∵△MNB是直角三角形,
∴![]()
又CM=BN
∴![]()
即![]() ,②正确;
,②正确;
∵∠CON=90°+∠BON, ∠DOM=90°+∠COM,∠BON=∠COM
∴∠CON=∠DOM
又CO=DO, ON=OM,
∴![]() ,③正确;
,③正确;
④∵AB=2,
∴S正方形ABCD=4,
∵△OCM≌△OBN,
∴四边形BMON的面积=△BOC的面积=1,即四边形BMON的面积是定值1,
∴当△MNB的面积最大时,△MNO的面积最小,
设BN=x=CM,则BM=2x,
∴△MNB的面积=![]() x(2x)=
x(2x)= ![]() x2+x=
x2+x= ![]() (x1)2+
(x1)2+![]() ,
,
∴当x=1时,△MNB的面积有最大值![]() ,
,
此时S△OMN的最小值是1 ![]() =
=![]() ,
,
故④不正确;


科目:初中数学 来源: 题型:
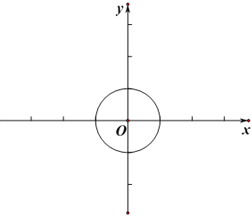
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下的定义:若⊙C上存在两个点A、B,使得∠APB=60°,则称P为⊙C的可视点.
(1)当⊙O的半径为1时,
①在点![]() 、E(1,1)、F(3,0)中,⊙O的可视点是______.
、E(1,1)、F(3,0)中,⊙O的可视点是______.
②过点M(4,0)作直线l:y=kx+b,若直线l上存在⊙O的可视点,求b的取值范围;
(2)若T(t,0),⊙T的半径为1,直线y=![]() 上存在⊙T的可视点,且所有可视点构成的线段长度为n,若
上存在⊙T的可视点,且所有可视点构成的线段长度为n,若![]() ,直接写出t 的取值范围.
,直接写出t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
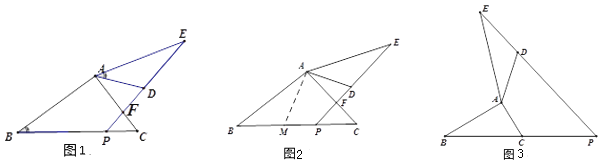
小明同学遇到这样一个问题,如图1,AB=AE,∠ABC=∠EAD,AD=mAC,点P在线段BC上,∠ADE=∠ADP+∠ACB,求![]() 的值.
的值.
小明研究发现,作∠BAM=∠AED,交BC于点M,通过构造全等三角形,将线段BC转化为用含AD的式子表示出来,从而求得![]() 的值(如图2).
的值(如图2).
(1)小明构造的全等三角形是:_________≌________;
(2)请你将小明的研究过程补充完整,并求出![]() 的值.
的值.
(3)参考小明思考问题的方法,解决问题:
如图3,若将原题中“AB=AE”改为“AB=kAE”,“点P在线段BC上”改为“点P在线段BC的延长线上”,其它条件不变,若∠ACB=2α,求:![]() 的值(结果请用含α,k,m的式子表示).
的值(结果请用含α,k,m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
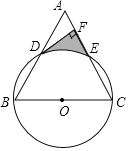
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
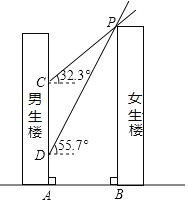
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片 ABCD 中,AD=5cm,AB=4cm,将矩形纸片 ABCD 沿直线l 折叠,使点 A 落在边 BC 上的 A'处,当直线 l 恰好过点 D 时,用直尺和圆规在图中作出直线 l,(保留作图 痕迹,不写作法),设点 A'与点 B 的距离为 x cm.并求出 x 的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】白天,小明和小亮在阳光下散步,小亮对小明说:“咱俩的身高都是已知的.如果量出此时我的影长,那么我就能求出你此时的影长.”晚上,他们二人有在路灯下散步,小明想起白天的事,就对小亮说“如果量出此时我的影长,那么我就能求出你此时的影长”.你认为小明、小亮的说法有道理吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
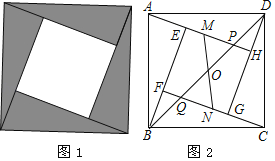
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com