
【题目】白天,小明和小亮在阳光下散步,小亮对小明说:“咱俩的身高都是已知的.如果量出此时我的影长,那么我就能求出你此时的影长.”晚上,他们二人有在路灯下散步,小明想起白天的事,就对小亮说“如果量出此时我的影长,那么我就能求出你此时的影长”.你认为小明、小亮的说法有道理吗?说说你的理由.
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
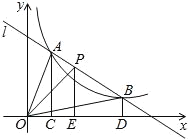
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
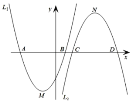
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 与
与![]() 的交点,
的交点,![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 作
作![]() 垂直
垂直![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值是1.其中正确结论是( )
的最小值是1.其中正确结论是( )
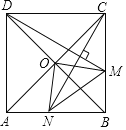
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
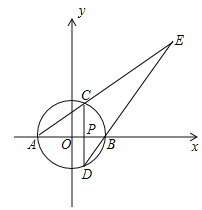
【题目】如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
(1)求点P的坐标;
(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个箱子内有![]() 颗相同的球,将
颗相同的球,将![]() 颗球分别标示号码
颗球分别标示号码![]() ,
,![]() ,
,![]() ,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球
,今浩浩以每次从箱子内取一颗球且取后放回的方式抽取,并预计取球![]() 次,现已取了
次,现已取了![]() 次,取出的号码依次为
次,取出的号码依次为![]() ,
,![]() ,
,![]() ,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球
,若每次取球时,任一颗球被取到的机会皆相等,且取出的号码即为得分数,浩浩打算依计划继续从箱子取球![]() 次,则发生“这
次,则发生“这![]() 次得分的平均数在
次得分的平均数在![]() 之间(含
之间(含![]() ,
,![]() )”的情形的概率为________.
)”的情形的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上运动(不运动至两端点),射线
上运动(不运动至两端点),射线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的外接圆,连结
的外接圆,连结![]() ,
,![]() ,
,![]() .
.
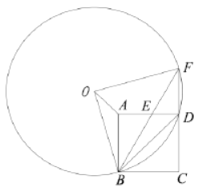
(1)求![]() 的度数.
的度数.
(2)求证:![]() .
.
(3)若正方形![]() 的边长为
的边长为![]() .
.
①当![]() 为
为![]() 中点时,求四边形
中点时,求四边形![]() 的面积.
的面积.
②设![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() _________(直接写出答案).
_________(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
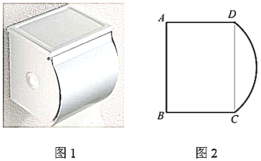
【题目】如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,圆弧盖板侧面
,圆弧盖板侧面![]() 所在圆的圆心
所在圆的圆心![]() 是矩形
是矩形![]() 的中心,绕点
的中心,绕点![]() 旋转开关(所有结果保留小数点后一位).
旋转开关(所有结果保留小数点后一位).
(1)求![]() 所在
所在![]() 的半径长及
的半径长及![]() 所对的圆心角度数;
所对的圆心角度数;
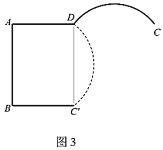
(2)如图3,当圆弧盖板侧面![]() 从起始位置
从起始位置![]() 绕点
绕点![]() 旋转
旋转![]() 时,求
时,求![]() 在这个旋转过程中扫过的的面积.
在这个旋转过程中扫过的的面积.
参考数据:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com