
【题目】如图,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上运动(不运动至两端点),射线
上运动(不运动至两端点),射线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 的外接圆,连结
的外接圆,连结![]() ,
,![]() ,
,![]() .
.
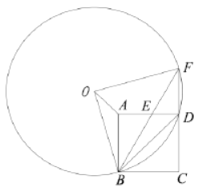
(1)求![]() 的度数.
的度数.
(2)求证:![]() .
.
(3)若正方形![]() 的边长为
的边长为![]() .
.
①当![]() 为
为![]() 中点时,求四边形
中点时,求四边形![]() 的面积.
的面积.
②设![]() ,
,![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 平分
平分![]() 时,
时,![]() _________(直接写出答案).
_________(直接写出答案).
【答案】(1)45°;(2)见解析;(3)①3,②![]()
【解析】
(1)根据正方形的性质和弧的度数等于弧所对的圆心角的度数,即可求出![]() .
.
(2)可证得△OAB≌△OAD,求出∠OAD度数,∠OFB=45°,在四边形OADF中,利用四边形内角和,即可证得![]() .
.
(3)①四边形OAEF的面积=△OAD的面积+△ODF的面积-△FDE的面积,作OH⊥AD,OG⊥FD,垂足分别为H,G,连结OD,分别求得△OAD的面积、△ODF的面积和△FDE的面积,即可求解.
②可证得∴![]() 所以
所以![]() ,
,![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,它们的高均为MD,为求面积比,即可求来
,它们的高均为MD,为求面积比,即可求来![]() ,设圆的半径为r,可将BE、ME、MF均用r表示出来即可求解.
,设圆的半径为r,可将BE、ME、MF均用r表示出来即可求解.
(1) 解:∵∠ADB=45°, ∠ADF=90°,
∴∠BDF=135°
∴优弧![]() =270°.
=270°.
∴![]() =90°,∠BOF =90°
=90°,∠BOF =90°
∵OB=OF,
∴∠OFB=∠OBF=45°
故答案为:45°
(2)证明:连结OD(如图1),
∵OB=OD,OA=OA,AB=AD,
∴△OAB≌△OAD(SSS).
∴∠OAB=∠OAD=![]() .
.
∵∠OFB=45°,
∴∠AOF+∠AEF=360°-135°-45°=180°
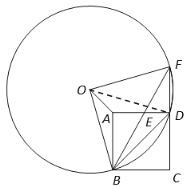
图1
(3)①作OH⊥AD,OG⊥FD,垂足分别为H,G,连结OD(如图2),
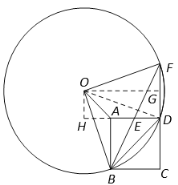
图2
由AE=ED,易得△ABE≌△DFE,
∴FD=AB=2,
由OD=OF,OG⊥FD,得GD=![]()
由OH⊥AD,OG⊥FD,∠ADF=90°,得矩形OHDG,
∴OH=GD=1.
由∠OAH=∠OAB-∠HAB=135°-90°=45°,
得∠HOA=∠HAO=45°
∴AH=OH=1,OG=HD=AH+AD=1+2=3.
∵△OAD的面积=![]() ,
,
△ODF的面积=![]() ,
,
△FDE的面积=![]() ,
,
∴四边形OAEF的面积=△OAD的面积+△ODF的面积-△FDE的面积=1+3-1=3.
②OD与BF交于点M如图3:
![]() 平分
平分![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∵OF=OB
∴BM=MF
设圆的半径为r
BM=MF=![]()
∵![]()
∵![]()
∴![]()
∴![]()
![]()
![]() ,
,![]()
![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,三个三角形的高均为MD
,三个三角形的高均为MD
∴![]()

图3
故答案为:![]()


科目:初中数学 来源: 题型:
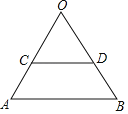
【题目】如图,△ABO是正三角形,CD∥AB,把△ABO绕△OCD的内心P旋转180°得到△EFG
(1)在图中画出点P和△EFG,保留画图痕迹,简要说明理由
(2)若AO=3![]() ,CD=2
,CD=2![]() ,求A点运动到E点路径的长.
,求A点运动到E点路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
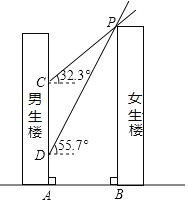
【题目】如图,男生楼在女生楼的左侧,两楼高度均为90m,楼间距为AB,冬至日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为
,女生楼在男生楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为![]() ,女生楼在男生楼墙面上的影高为DA,已知
,女生楼在男生楼墙面上的影高为DA,已知![]() .
.
![]() 求楼间距AB;
求楼间距AB;
![]() 若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?
若男生楼共30层,层高均为3m,请通过计算说明多少层以下会受到挡光的影响?![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】白天,小明和小亮在阳光下散步,小亮对小明说:“咱俩的身高都是已知的.如果量出此时我的影长,那么我就能求出你此时的影长.”晚上,他们二人有在路灯下散步,小明想起白天的事,就对小亮说“如果量出此时我的影长,那么我就能求出你此时的影长”.你认为小明、小亮的说法有道理吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中
中![]() ,
,![]() 是
是![]() 的中点.请按要求完成下列作图,
的中点.请按要求完成下列作图,
①仅用无刻度直尺,不能用直尺中的直角;②保留作图痕迹
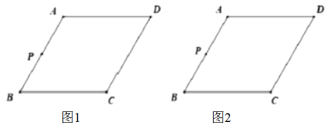
(1)在图1中,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 交于点
交于点![]() .
.
(2)在图2中,作线段![]() 的中垂线,垂足为点
的中垂线,垂足为点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AOBC放置在平面直角坐标系xOy中,边OA在y轴的正半轴上,边OB在x轴的正半轴上,抛物线的顶点为F,对称轴交AC于点E,且抛物线经过点A(0,2),点C,点D(3,0).∠AOB的平分线是OE,交抛物线对称轴左侧于点H,连接HF.
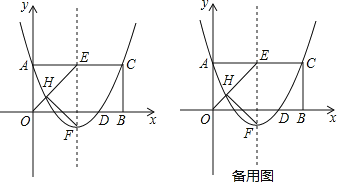
(1)求该抛物线的解析式;
(2)在x轴上有动点M,线段BC上有动点N,求四边形EAMN的周长的最小值;
(3)该抛物线上是否存在点P,使得四边形EHFP为平行四边形?如果存在,求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
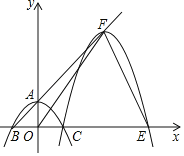
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com